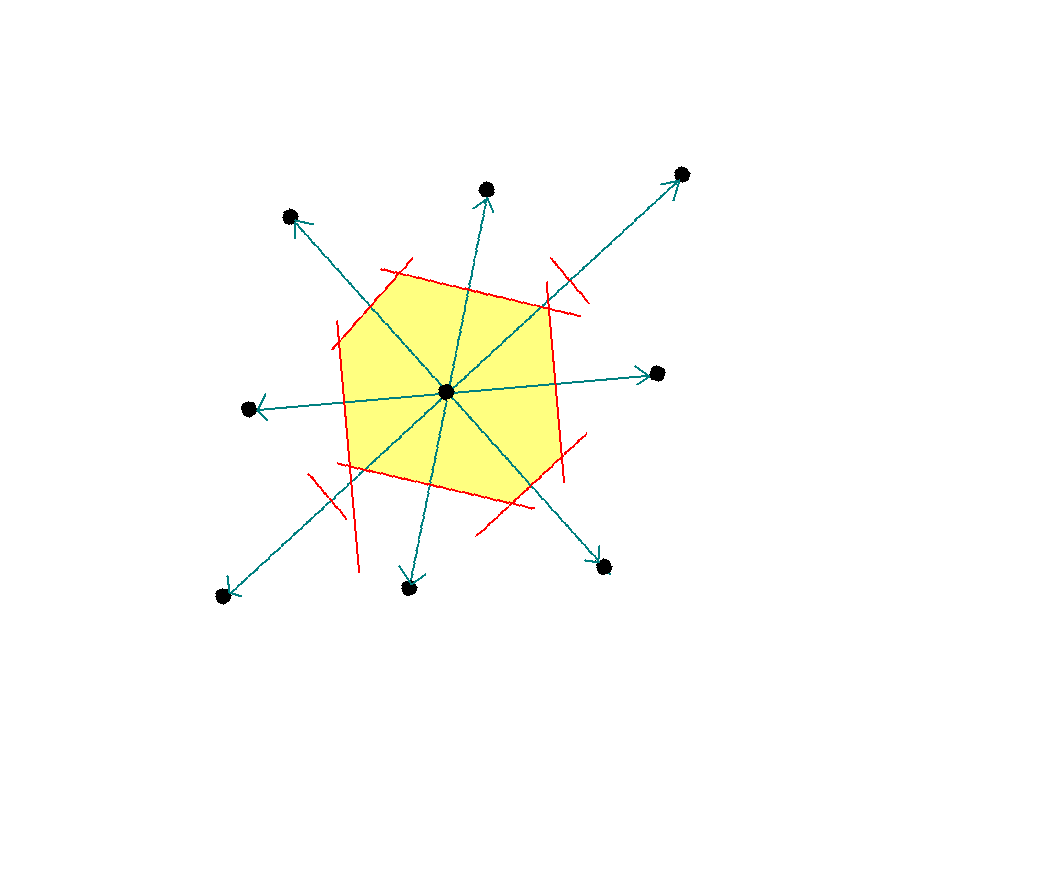
* A Brillouin zone is defined as a Wigner-Seitz cell in the reciprocal lattice. If we consider the lattice points in the figure as belonging to the reciprocal and follow the same steps as outlined we will have constructed the Wigner-Seitz primitive cell of the reciprocal lattice. The lines joining the origin of the lattice to the neighbouring lattice points now represent the reciprocal lattice vectors G.

The smallest area enclosed by the Weigner-Seitz cell (in yellow) is also known as the first Brillouin zone.
We could use the same procedure as outlined earlier to construct the first Brillouin zone of a linear lattice, a square lattice or a cubic lattice.
The Bragg diffraction law
![]()
can be understood in terms of the Brillouin zone. Recall from the figure of the Ewald sphere that the reciprocal lattice vector G is bisected perpendicularly by the reflecting plane EBH and the wave vector k has one of its tips at the origin and the other tip touches this plane. This G, k combination satisfies the above Bragg equation. Extrapolating to three-dimensions, the set of planes which are perpendicular bisectors of the reciprocal lattice vectors Gs and on which the tips of the wave vectors k just touch, satisfy Bragg's condition for diffraction. These planes divide the reciprocal lattice space into small areas in two-dimension or volumes in three-dimensions which in turn are called Brillouin zones. The smallest of them is nothing but the primitive cell of the reciprocal lattice.
Lets now take a graphical illustration to understand things better.
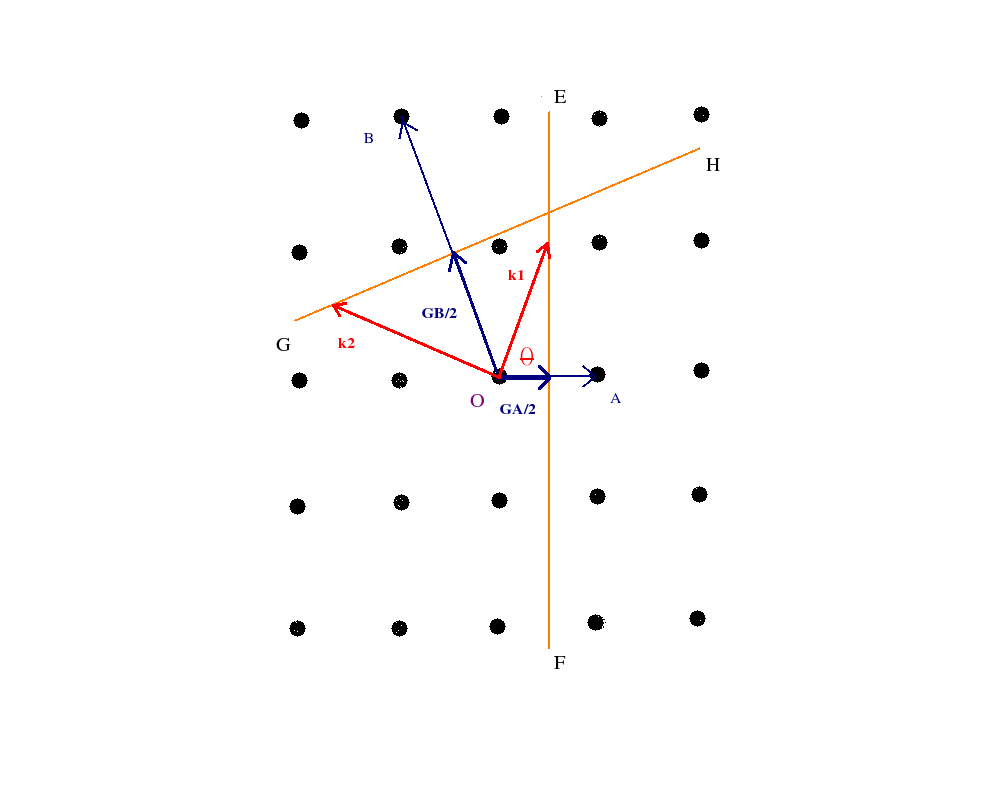
GA and GB are reciprocal lattice vectors which are bisected normally by the planes EF and GH respectively. The wave vectors k1 and k2 start from the origin O of the lattice and just touch the two planes EF and GH respectively.
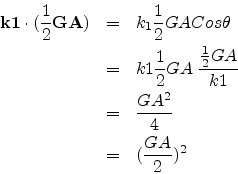
Thus k1 and GA satisfy the Bragg condition. Same can be proved for k2 and GB. Thus the two planes EF and GF form some sort of zone boundaries which have to be touched by the tip of the wave vectors from the common origin O for Bragg condition to be satisfied. When we take more such boundaries we have an enclosed area or volume which we call the Brillouin zone.