Brillouin zones of different lattices

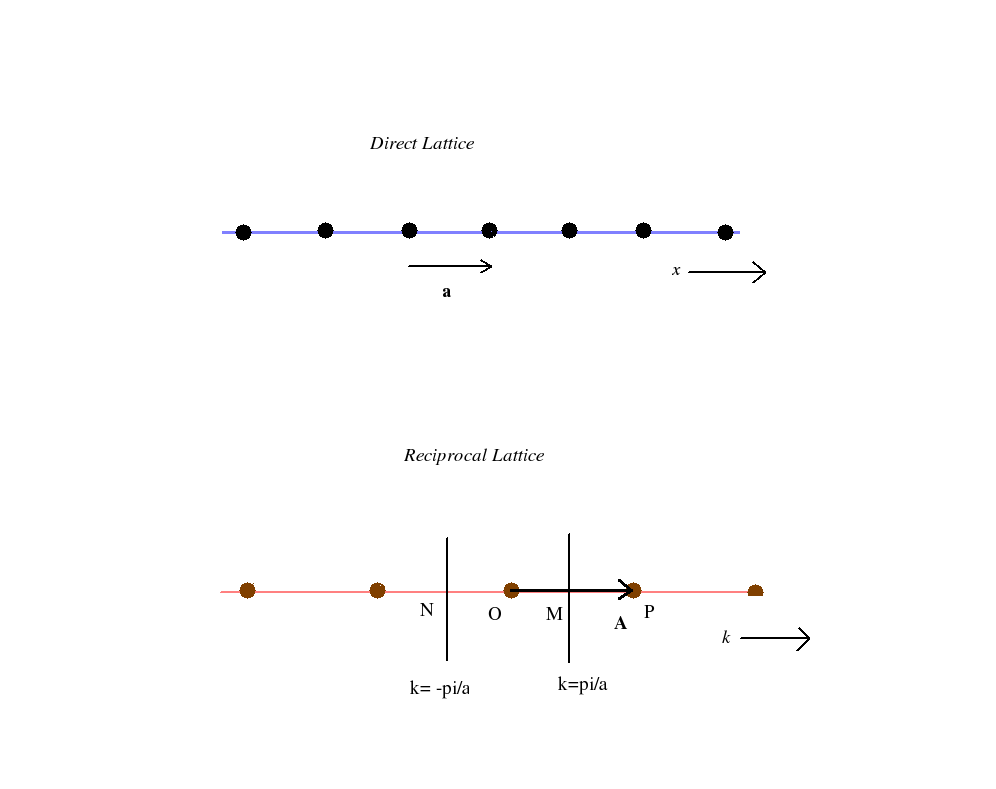
Let us see how we may construct the Brilloin zones for different lattices. We start with a one dimensional linear lattice for which the direct lattice translational vector T = a where a is the only basis vector of the direct lattice. The reciprocal lattice for this linear direct lattice would also be linear as shown below.

Then the reciprocal lattice vector G equals A where A is the only basis vector for the one dimensional reciprocal lattice. In the figure OP = A. The two normals bisecting A on either side of the origin at the points M and N specify the boundaries of the brillouin zone.

From the equations relating the basis vectors in the two lattices, we find that A ^. a=2$\pi$. In this case Aa = 2$\pi$ or A = (2$\pi$/a). Therefore

$$\begin{eqnarray*} {\mathbf {k}}\cdot(\frac{1}{2}{\mathbf {G}}) & = & (\frac{1}{2... ...f {k}}\cdot(\frac{1}{2}{\mathbf {A}}) & = & (\frac{1}{2} A)^{2} \end{eqnarray*}$$

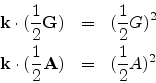
Since k can occur on both sides of the origin

$$\begin{eqnarray*} \frac{+}{\minus}\frac{1}{2} kA & = & \frac{A^{2}}{4} \\ k & =... ...minus}\frac{2\pi}{2a} \\ \; & = & \frac{+}{\minus}\frac{\pi}{a} \end{eqnarray*}$$

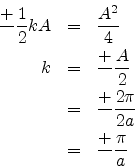
Thus the Brillouin zone of a one dimensional linear lattice is specified by the two points $${\frac{{+}}{{\minus}}}$$($$\pi$$/a).

Similarly we may find that the first Brillouin zone of a square reciprocal lattice which is the primitive cell in the reciprocal lattice is also a square of sides (2$\pi$/a) centred at the origin.

The reciprocal lattice of a simple cubic crystal obtained from the equations relating the basis vectors in the two lattices is found to be another simple cubic lattice. If the magnitude of the basis vectors of the direct lattice be a then that for the reciprocal lattice is (2$\pi$/a). The first Brillouin zone is found to be a cube bounded by six planes which bisect the six smallest reciprocal lattice vectors. The length of each side of the cube is again (2$\pi$/a).

Working on similar lines it can be found that the reciprocal lattice of a bcc lattice is a face centred lattice and the corresponding first Brillouin zone is a regular rhombic dodecahedron.

Also the reciprocal lattice of an fcc lattice is a body centred lattice and the corresponding first Brillouin zone is a truncated octahedron.

Refer Kittel's Introduction to solid state physics for good pictures of the Brillouin zones.