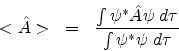
Now that we know something about what operators are in quantum mechanics lets see how they may be used to connect quantum mechanics with experimental measurements.
The first of the related postulates states that when a series of measurements is made of a physical observable A, then average or mean value of the measurements is equal to the expectation value of the operator  corresponding to the physical observable A and is given by
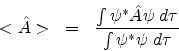
Here ![]() is the wave function describing the system in question. If
is the wave function describing the system in question. If ![]() is normalized then the expectation value is given by
is normalized then the expectation value is given by
![]()
If ![]() is an eigenfunction of the operator  with eigenvalue a then each of the measurements of the physical observable A would be equal to the eigenvalue a.
is an eigenfunction of the operator  with eigenvalue a then each of the measurements of the physical observable A would be equal to the eigenvalue a.
However if ![]() is not an eigenfunction of the operator Â, yet is an eigenfunction of the Hamiltonian
is not an eigenfunction of the operator Â, yet is an eigenfunction of the Hamiltonian ![]() , it can be expressed as a linear combination of the eigenfunctions
, it can be expressed as a linear combination of the eigenfunctions ![]() of  with eigenvalues an as:
of  with eigenvalues an as:
![]()
![]()
bn are the corresponding coefficients.
Then a single measurement of the physical observable  would yield any one of the eigenvalues an and the average of many such measurements would be equal to the weighted sum of the corresponding eigenvalues, i.e.,
![]()
This is the essence of the other postulate related to the use of operators in quantum mechanics.