In an experiment performed by the Dutch physicist Peter Zeeman in 1896, it was observed that each spectral line in the excitation spectrum for an atom placed in a magnetic field split into number of additional lines. Furthermore, the difference in energy between the new lines and the original line was found to be directly proportional to the strength of the external field. This effect came to be known as Zeeman effect. It could only be explained using quantum mechanics which says that the orbital angular momentum is quantized both in magnitude and direction:
|![]() | =
| = ![]()
![]() and
Lz = ml
and
Lz = ml![]()
We now shall try to understand the normal Zeeman effect more fully.
At first let us formulate a few classical expressions associated with an electron moving in a circular path around a nucleus as shown in the animation.
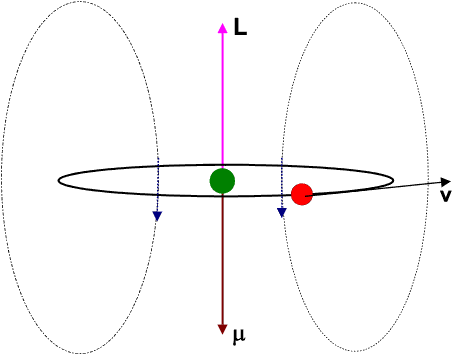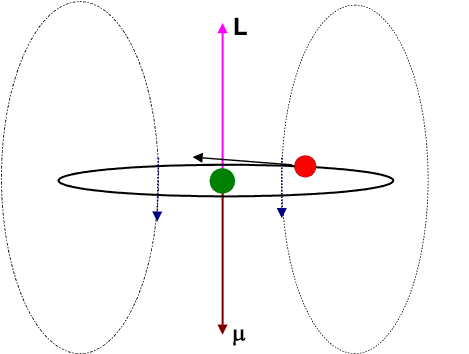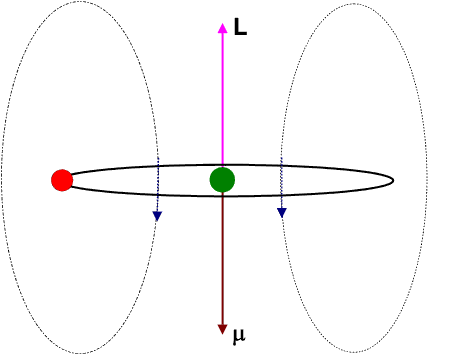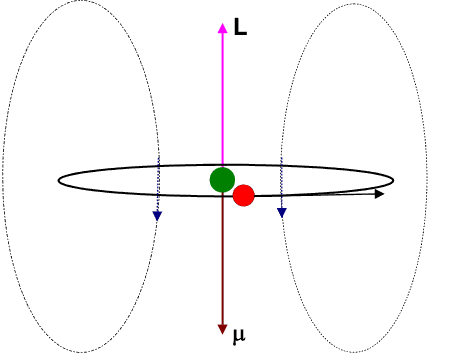
The circulating electron would create a magnetic field and hence give rise to a magnetic dipole moment ![]() . It is left for the students to derive the relation betwen
. It is left for the students to derive the relation betwen ![]() and the orbital angular momentum (
and the orbital angular momentum (![]() ) of the electron:
) of the electron:
![]()
Now if the current loop is placed in an external manetic field (along the z direction (say)), then the torque ![]() on the magnetic dipole is
on the magnetic dipole is
![]()
and the coresponding potential energy is given by
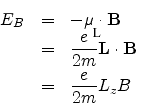
According to quantum mechanics
Lz = ml![]() . Therefore the total energy is
. Therefore the total energy is
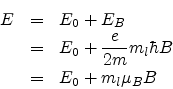
E0 is the energy in the absence of the field and
![]() =
= ![]()
![]() is called the Bohr magneton, having dimensions the same as the dipole moment
is called the Bohr magneton, having dimensions the same as the dipole moment ![]() .
.
Thus each energy level splits into 2l + 1 levels, since ml=-l to +l in integral steps.
The emission spectrum of the atom placed in the external magnetic field ![]() will however show only two additional lines apart from the original line. This is because the selection rules for electric dipole transitions are
will however show only two additional lines apart from the original line. This is because the selection rules for electric dipole transitions are
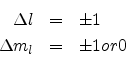
The frequency or wavelength of the three lines can be obtained from the relations
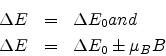
The two symmetricaly placed lines on either side of the zero-field line are shifted in energy by ![]() B.
These three lines constitute what is known as a triplet.
B.
These three lines constitute what is known as a triplet.
The Zeeman effect may also be explained in terms of a vector model as shown in the following figure.
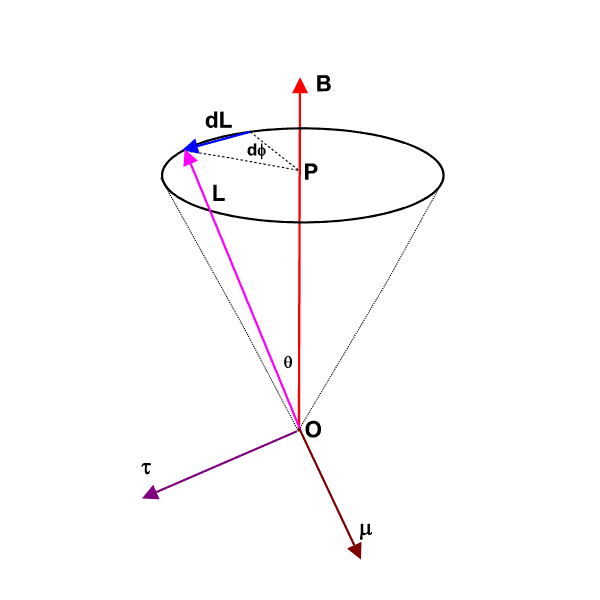
The magnetic dipole moment ![]() of the electron is antiparallel to the orbital angular momentum
of the electron is antiparallel to the orbital angular momentum ![]() . Both precess around the constant magnetic field
. Both precess around the constant magnetic field ![]() with an angular frequency of precession proportional to the field-strength and given by
with an angular frequency of precession proportional to the field-strength and given by
This precession is called Larmor precession.
![]() is also equal to the frequency shift of the Zeeman lines originating from the external field from the field-free line. This precession of the
is also equal to the frequency shift of the Zeeman lines originating from the external field from the field-free line. This precession of the ![]() around
around ![]() is shown in the following animation.
is shown in the following animation.
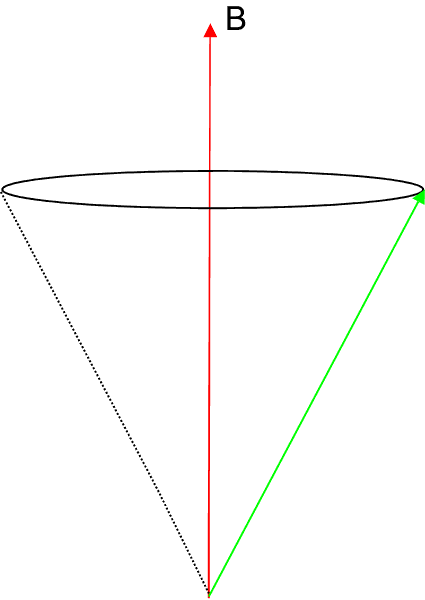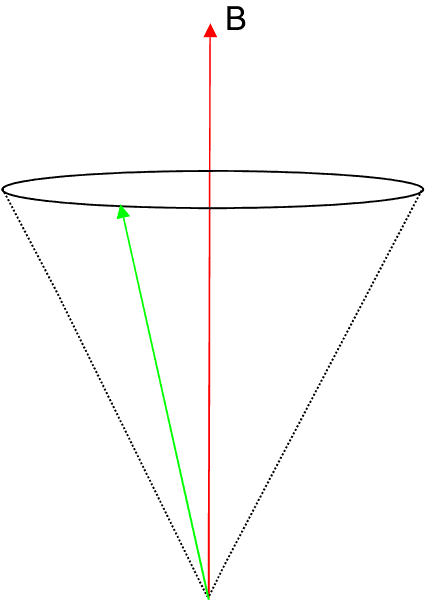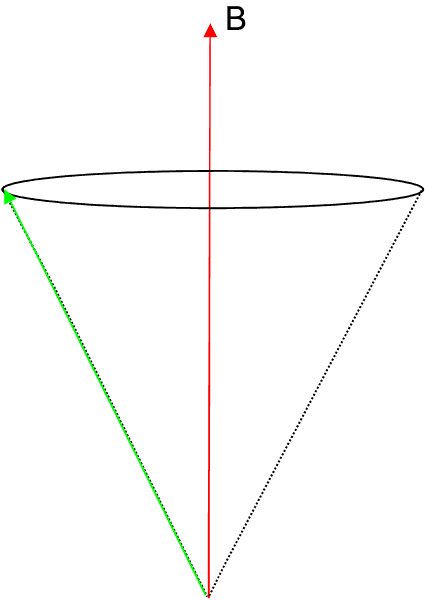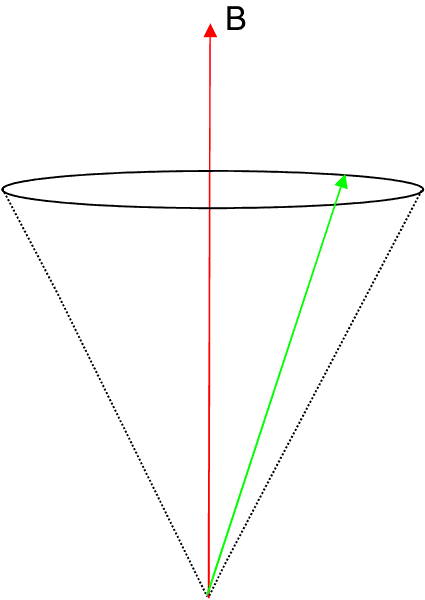
Note that for (2l + 1) different values of ml we have (2l + 1) different values of the projection of ![]() , viz.,
Lz = ml
, viz.,
Lz = ml![]() or (2l + 1) different values of
or (2l + 1) different values of ![]() . This aspect is referred to as space quantization of the orbital angular momentum in the presence of an external field.
. This aspect is referred to as space quantization of the orbital angular momentum in the presence of an external field.