The emission spectrum of hydrogen has to do with transition between different energy levels characterized by different values of the principal quantum number n, since,
![]()
However the emission spectrum of hydrogen showed fine strucure, i.e. additional lines which could not be accounted for as above. Bohr and Sommerfield's theory with elliptic orbits and with relativistic correction did however correctly explain this fine structure.
But again, even this theory could not account for the fine structure in the spectra of alkali atoms.
After the introduction of electron-spin by Uhlenbeck, Goudsmit and Dirac, originated the concept of spin-orbit coupling to account for the fine structure of spectral lines.
Let us view the current-loop animation again.
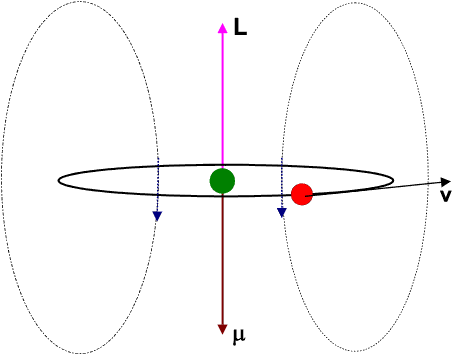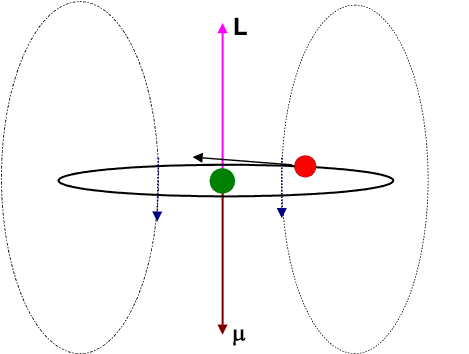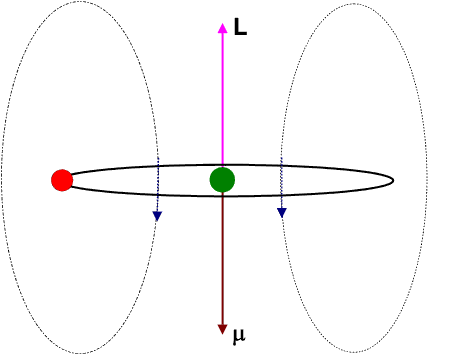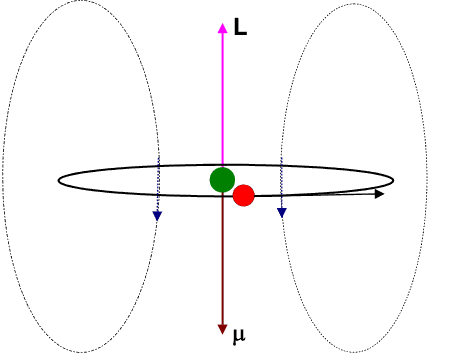
However, now, visualize the electron to be at rest at the centre and the charged nucleus (having an effective charge + | e|) to be revolving around it. This will result in an internal magnetic field (
![]() ) at the position of the electron, having the same direction as the orbital angular momentum
) at the position of the electron, having the same direction as the orbital angular momentum ![]() .
.
The blue arrows depicting the magnetic field should therefore be directed opposite to that shown in the figure. Moreover the magnetic dipole moment shown in the figure represents that moment which would produce an identical magnetic field as that produced by the circulating electron having angular momentum
![]() . It should not be confused with the the intrinsic spin magnetic dipole moment
. It should not be confused with the the intrinsic spin magnetic dipole moment
![]() which would have different orientations with respect to the internal magnetic field
which would have different orientations with respect to the internal magnetic field
![]() ,
and would interact with it to yield different values for the potential energy of interaction, viz.,
,
and would interact with it to yield different values for the potential energy of interaction, viz.,
![]()
Now
![]() and
and ![]() are proportional. So are
are proportional. So are
![]() and
and ![]() , since
, since
![]()
Hence the interaction energy can be seen to be proportional to
![]() .
. ![]() .
.
This is known as spin-orbit coupling and the pertinent interaction energy explains the splitting of the energy levels and the consequent observation of the fine structure in the spectrum of alkali atoms which incidentally can be thought of as one-electron atoms (having a charged core of one postive electronic charge and a losely bound valence or optical electron).
As for example, the spin-orbit interaction explains the splitting of the sodium D line into two lines D1 (589.6nm) and D2 (589.0nm).
We can take recourse to the vector model of the one-electron atom to visualize spin-orbit interaction.
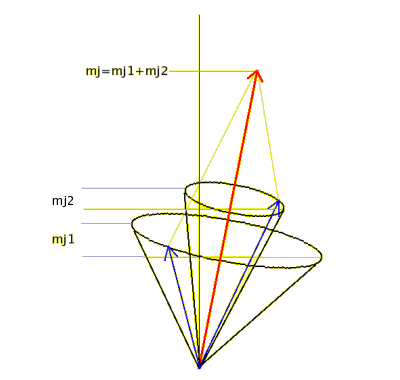
The blue arrows depict the orbital
![]() and spin
and spin ![]() angular momenta which therefore play the role of j1 and j2 in the coupled representation. mj1, mj1 become
ML and MS respectively. We may write the resultant magnetic quantum number mj as MJ.
angular momenta which therefore play the role of j1 and j2 in the coupled representation. mj1, mj1 become
ML and MS respectively. We may write the resultant magnetic quantum number mj as MJ.
![]() and
and ![]() magnetically interact producing torques on each other which in turn make the two vectors precess about their resultant
magnetically interact producing torques on each other which in turn make the two vectors precess about their resultant
![]() =
= ![]() +
+ ![]() . The angle between
. The angle between ![]() and
and ![]() remains constant ensuring that the magnitude and direction of
remains constant ensuring that the magnitude and direction of ![]() is kept constant too.
Note that ML and MS are no longer fixed but MJ=ML + MS is. The magnitude of the resultant angular momentum is given by
is kept constant too.
Note that ML and MS are no longer fixed but MJ=ML + MS is. The magnitude of the resultant angular momentum is given by
![]() .
.
The quantum number J can be found from the quantum numbers L and S through the Clebsch Gordon series and MJ is obtained from J as before.
It is important to note that the vector model which we have been discussing so far applies to a one-electron or an equivalent single electron atom. However it can be extended to a many electron atom as well. Such a system would have an inert core containing tightly bound electrons in completely filled subshells surrounding the nucleus along with one or more electrons in loosely bound outer subshell or subshells. These electrons are called optically active electrons as optical excitations are possible between energy levels belonging to them.
In many electron atoms as described above, the coupling of the orbital and spin angular momenta of each atom follows two coupling schemes. For light and medium heavy atoms, we employ LS coupling or Russel-Saunders coupling and for heavy atoms we use jj-coupling.
In LS coupling, the orbital and spin angular momenta of the individual electrons seperately couple to form net orbital and net spin angular momenta respectively. These two then couple to form the total angular momentum ![]() .
.
Here we consider only atoms in which the outermost shell is less than half filled.
The main contribution to the energy of these optically active electrons comes from the strong interaction between them which, according to Hartree approximation, depends only on the quantum numbers n and l. In this approximation, each optically active electron moves under a mean potential of all other such electrons. Now, for every l, there are (2l+1) ml values and for each ml value, there are 2 ms values. In all there are many degenerate energy states having the same energy.
The degeneracies are removed (i.e. each energy level is split up) when we consider weaker interactions like residual coulomb interaction (the part of the coulomb interaction missing in Hartree approximation) and spin-orbit interaction.
Due to residual Coulomb attraction the spin angular momenta of the optically active electrons couple so that the resultant spin angular momentum's magnitude |![]() | becomes constant and the energy of the system is generally lowest for the state in which |
| becomes constant and the energy of the system is generally lowest for the state in which |![]() | is largest.
| is largest.
Again, due to residual Coulomb attraction the orbital angular momenta of the optically active electrons couple so that the resultant orbital angular momentum's magnitude |![]() | becomes constant and the energy of the system is generally lowest for the state in which |
| becomes constant and the energy of the system is generally lowest for the state in which |![]() |
is largest.
|
is largest.
And finally, due to spin-orbit interaction, which we have already studied for one-electron systems, ![]() and
and ![]() couple together to form the total angular mometum
couple together to form the total angular mometum ![]() of the composite system such that its magnitude |
of the composite system such that its magnitude |![]() | remains constant and the energy of the system is lowest for the case where |
| remains constant and the energy of the system is lowest for the case where |![]() | is smallest.
| is smallest.
The pertinent equations are
![]()
![]()
![]()
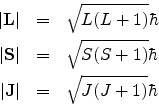
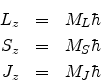
The quantum numbers L, S and J can be found from the Clebsch Gordon series and ML, MS and MJ can be obtained from L, S and J respectively as before.
In the vector model, the vectors ![]() and
and ![]() precess around in their respective cones around the total angular momentum vector
precess around in their respective cones around the total angular momentum vector ![]() . The picture is similar to the vector model for the one-electron spin-orbit coupling, except that the individual spin and individual orbital momentum vectors of each optically active electron first couple among themselves to respectively form the resultant spin angular momentum and resultant orbital angular momentum vectors. In doing so the individual spin and orbital angular momentum vectors precess in their own respective cones around the respective resultant vectors. These precessions are relatively faster since they represent relatively stronger interaction. It is these latter resultant vectors that precess in their respective cones around the composite total angular momentum vector
. The picture is similar to the vector model for the one-electron spin-orbit coupling, except that the individual spin and individual orbital momentum vectors of each optically active electron first couple among themselves to respectively form the resultant spin angular momentum and resultant orbital angular momentum vectors. In doing so the individual spin and orbital angular momentum vectors precess in their own respective cones around the respective resultant vectors. These precessions are relatively faster since they represent relatively stronger interaction. It is these latter resultant vectors that precess in their respective cones around the composite total angular momentum vector ![]() . As can be guessed, this precession occurs slowly because of the relatively weak spin-orbit interaction.
. As can be guessed, this precession occurs slowly because of the relatively weak spin-orbit interaction.
The expression for the energy of each fine-structure level, as it is called, corresponding to the quantum numbers S, L and J is given by
DeltaE= C [(J(J+1) - L(L+1)-S(S+1)]
where C is a constant.
When no external field is present, the energy of the system (atom) is independent of the quantum number Mj. The reverse is also true as we shall explore in the next section.
When one or more electron jumps from one enrgy level to another optical transitions of fixed wavelength occur. However these transitions are constrained by what are called selection rules for strong electric dipole transitions in multi-electron atoms:
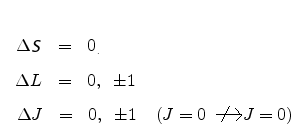
The seperation in energy between adjacent lines in the multiplet (different J values) spectrum can be found from the expression of DeltaE above as follows:
E=2C(J+1) where J+1 and J represent the total angular momentum quantum numbers for the upper and lower energy levels respectively.
And finally in jj - coupling , the orbital and spin angular momentum of each individual electron at first couple to form a net angular momentum
![]() for each electron. All the
for each electron. All the
![]() then couple to form the total angular momentum
then couple to form the total angular momentum ![]() . This happens in heavy atoms with large atomic number (Z) values where the spin-orbit interaction becomes the dominant interaction as opposed to the residual interaction.
. This happens in heavy atoms with large atomic number (Z) values where the spin-orbit interaction becomes the dominant interaction as opposed to the residual interaction.