Stationary states

From the previous section we observe that for systems for which the potential energy itself does not depend on time, the modulus square of the wave function $$\begin{eqnarray*} \Psi(x,t) & & \end{eqnarray*}$$ given by

$$\begin{eqnarray*} \vert\Psi(x,t)\vert^{2} & = & \Psi^{*}(x,t) \Psi(x,t) \\ & = & \vert\psi(x)\vert^{2} \end{eqnarray*}$$

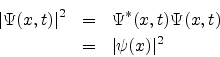
Thus the probability density is independent of time. The state of the system represented by

$$\begin{eqnarray*} \Psi(x,t) & = & \psi(x)\times e^{-iEt/\hbar } \end{eqnarray*}$$.

is called a stationary state.