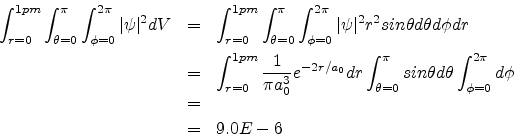Problems

Problem 1:

The ground state wavefunction for a particle in a one-dimensional box of length L is

$$\begin{eqnarray*} \psi & = & \sqrt{\frac{2}{L}} sin \frac{\pi x}{L} \end{eqnarray*}$$

Suppose the box is 10.0nm long. Calculate the probability that the particle is between x=4.95 nm and 5.05 nm.

Solution:

The probability of finding the particle between x and x + dx is given by $$\begin{eqnarray*} \vert\psi\vert^{2}dx & & \end{eqnarray*}$$. Therefore the required probability is

$$\begin{eqnarray*} \int_{x=4.95}^{5.05} {\vert\psi\vert^{2}}dx & = & \int_{x=4.95... ...}\int_{x=4.95}^{5.05} (1-cos \frac{2\pi x}{L}) dx \\ & = & 0.02 \end{eqnarray*}$$

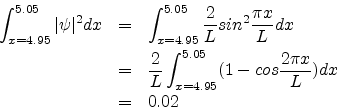
Problem 2:

The ground state wave function of the hydrogen atom is given by

$$\begin{eqnarray*} \psi & = & (\frac{1}{\pi a_{0}^{3}})^{1/2}e^{-r/a_0} \end{eqnarray*}$$

a₀ = 0.53A⁰ is the Bohr radius. Calculate the probability that the electron would be found somewhere within a small sphere of radius 1pm centred at the nucleus.

Solution:

The required probability is

$$\begin{eqnarray*} \int_{r=0}^{1pm} \int_{\theta=0}^{\pi} \int_{\phi=0}^{2\pi} {\... ...ta d\theta \int_{\phi=0}^{2\pi} d\phi \\ & = & \\ & = & 9.0E-6 \end{eqnarray*}$$