Density functional theory (DFT) is an alternative prescription of quantum mechanics, which uses, instead of the traditional many electron wave function ![]() the one electron density function
the one electron density function ![]() to describe a
physical or a chemical system. Such a system may be an atom, a molecule, an ion, a radical or several molecules in a state of interaction. For an N-electron system,
to describe a
physical or a chemical system. Such a system may be an atom, a molecule, an ion, a radical or several molecules in a state of interaction. For an N-electron system,
![]()
The basic understanding in DFT that the energy of an electronic system can be expressed in terms of its density dates back to the early work of Thomas and Fermi. In their atomic model the kinetic and potential energy are expressed in terms of ![]() . In spite of being highly approximate, the conceptual as well as computational expedience of the Thomas-Fermi method has ensured its wide applicability in atomic physics. On the other hand the first density based scheme to be used in more than one atom is the Hartree-Fock-Slater or X
. In spite of being highly approximate, the conceptual as well as computational expedience of the Thomas-Fermi method has ensured its wide applicability in atomic physics. On the other hand the first density based scheme to be used in more than one atom is the Hartree-Fock-Slater or X ![]() method. The method has its origin in solid state physics. Slater had proposed that the exchange potential of the electronic system can be represented by a function which is proportional to the one-third of the power of the density.
method. The method has its origin in solid state physics. Slater had proposed that the exchange potential of the electronic system can be represented by a function which is proportional to the one-third of the power of the density.
In 1964, Hohenberg and Kohn proved two theorems which vindicated the choice of
![]() (r) as a fundamental variable and put density functional theory on a firm footing.
(r) as a fundamental variable and put density functional theory on a firm footing.
The first theorem states that the non-degenerate ground state of an N-electron system moving under the influence of their mutual repulsion and an arbitrary external potential
V(r) is completely characterized by the one electron density
![]() (r).
(r).
Thus
![]() (r) determines the external potential
V(r) uniquely (to within an arbitrary constant) and an inverse mapping between the two,
(r) determines the external potential
V(r) uniquely (to within an arbitrary constant) and an inverse mapping between the two,
![]() (r)
(r) ![]() V(r), is found to exist. Since
V(r), is found to exist. Since
![]() (r) also determines N by integration, it also determines the full Hamiltonian (
(r) also determines N by integration, it also determines the full Hamiltonian (![]() ), and thereby, implicitly, all properties determined by
), and thereby, implicitly, all properties determined by
![]() . The N-particle ground state wave function
. The N-particle ground state wave function
![]() is one such property.
In other words,
V(r),
is one such property.
In other words,
V(r), ![]() and hence all ground state properties of the system can be expressed as unique functionals of
and hence all ground state properties of the system can be expressed as unique functionals of
![]() (
(![]() ). The second theorem says that, for a given external potential, the energy functional assumes a minimum value for the true density, i.e. a trial electron density,
). The second theorem says that, for a given external potential, the energy functional assumes a minimum value for the true density, i.e. a trial electron density,
![]() (r), which is not the exact
(r), which is not the exact
![]() (r),
will give an energy higher than the exact energy, E0.
(r),
will give an energy higher than the exact energy, E0.
The second theorem enables us to variationally determine the density ![]() and energy E by minimizing the energy functional E[
and energy E by minimizing the energy functional E[![]() ] with respect to the trial densities subject to the normalization constraint
] with respect to the trial densities subject to the normalization constraint
![]()
Therefore we have at our disposal the variational principle
![]()
where ![]() is the Lagrange multiplier or its simplified form, viz.,
is the Lagrange multiplier or its simplified form, viz.,
![]()
where
![]() is the functional derivative of E with respect to
is the functional derivative of E with respect to ![]() .
.
The above two equations are deterministic equations for
![]() (r) and are, as such, the pivotal equations of DFT. One needs to know, however, the functional form of E[
(r) and are, as such, the pivotal equations of DFT. One needs to know, however, the functional form of E[![]() ]. Following Hohenberg and Kohn , E[
]. Following Hohenberg and Kohn , E[![]() ] can be expressed as,
] can be expressed as,
![]()
where
V(![]() ) is the external potential as visualized by the electronic system and F[
) is the external potential as visualized by the electronic system and F[![]() ] is a universal functional which includes the contribution of the kinetic energy (T) and the electron-electron interaction energy Eee. Thus,
] is a universal functional which includes the contribution of the kinetic energy (T) and the electron-electron interaction energy Eee. Thus,
![]()
T[![]() ] is the kinetic energy functional, the integral term denotes the classical part of Eee or the coulomb self energy of the electrons and Exc represents the nonclassical part of Eee or the exchange-correlation (XC) energy of the electrons. Evaluation of E[
] is the kinetic energy functional, the integral term denotes the classical part of Eee or the coulomb self energy of the electrons and Exc represents the nonclassical part of Eee or the exchange-correlation (XC) energy of the electrons. Evaluation of E[![]() ], therefore, boils down to evaluating T[
], therefore, boils down to evaluating T[![]() ] and
Exc[
] and
Exc[![]() ]. Approximate forms of these functionals have been obtained by fashioning the behaviour of the actual inhomogeneous system on the basis of the homogeneous one. The main contribution to T[
]. Approximate forms of these functionals have been obtained by fashioning the behaviour of the actual inhomogeneous system on the basis of the homogeneous one. The main contribution to T[![]() ] comes from the Thomas-Fermi(TF) energy term, viz.,
] comes from the Thomas-Fermi(TF) energy term, viz.,
![]()
![]() .
.
The first correction to the above term is that due to Weizs![]() cker involving a gradient term, viz.,
cker involving a gradient term, viz.,
![]()
One of the most popular forms of the kinetic energy functional is
![]()
where TTF and TW have already been defined and $ is a multiplicative reduction factor. Goodisman, however, thought of T[![]() ] as a sum of
TW[
] as a sum of
TW[![]() ] and
] and
![]() (
(![]() , N) x TTF[
, N) x TTF[![]() ] where the correction factor
] where the correction factor
![]() (r, N) satisfied the boundary conditions
(r, N) satisfied the boundary conditions
![]() (r, N)
(r, N) ![]() 0 as
r
0 as
r ![]() 0 and
0 and
![]() (r, N)
(r, N) ![]() 1 as
r
1 as
r ![]()
![]() . Other higher order gradient corrections to T[
. Other higher order gradient corrections to T[![]() ] have also been suggested, the objective in all cases being the observation of maximum agreement between the total energy calculated using a good quality density function and the exact energy. With a view to construct approximate kinetic energy functionals with a good local behaviour, Ghosh and Deb have proposed a local kinetic energy functional, viz.,
] have also been suggested, the objective in all cases being the observation of maximum agreement between the total energy calculated using a good quality density function and the exact energy. With a view to construct approximate kinetic energy functionals with a good local behaviour, Ghosh and Deb have proposed a local kinetic energy functional, viz.,
![\begin{eqnarray}
T[\rho]= T_{TF}[\rho]+C_{x}\int \frac{\rho^{4/3}/r}{1+r\rho^{1/3}/0.043}\;d{\bf r}
\nonumber
\end{eqnarray}](elearningimg173.png)
![]() .
.
Chattaraj and Sengupta have put forward another atomic kinetic energy functional which accounts for proper global and local behaviour as well as a correct functional derivative, viz.,
![\begin{eqnarray}
\nonumber
T[\rho]=T_{TF}[\rho]+T_{W}[\rho]- a(N)\Xi \int\frac{\rho^{4/3}/r}{1+r\rho^{1/3}/0.043}\;d{\bf r},
\nonumber
\end{eqnarray}](elearningimg175.png)
![]() .
.
and a(N) is a constant dependent on the number of electrons, N.
In the case of a molecule like a diatomic, one needs to add another functional term to the atomic kinetic energy functional discussed above, viz.,
![]()
R being the internuclear distance.
The exchange-correlation (XC) energy Exc introduced earlier can be written in terms of the XC potential
Vxc(r) which in turn consists of two parts a) the Fermi exchange potential Vx which is a consequence of Pauli's exclusion principle and operates on electrons of the same spin and b) the Coulomb correlation potential Vc which is a reflection of the Coulomb interaction. Following the philosophy of local density approximation (LDA), in which one treats the electron gas as locally homogeneous, the exchange and correlation potentials and energies can be expressed as density functionals. Dirac proposed a
![]() -dependence of the exchange energy or in other words a
-dependence of the exchange energy or in other words a
![]() -dependence of the exchange potential. However, since this form has the shortcoming of not revealing proper asymptotic behaviour, corrections, like that of Becke have been introduced. The correlation potential on the other hand has been found to have a logarithmic dependence on density. However, other forms, Wigner type parametrized correlation energy functional being one of them, have also been applied in density functional calculations.
-dependence of the exchange potential. However, since this form has the shortcoming of not revealing proper asymptotic behaviour, corrections, like that of Becke have been introduced. The correlation potential on the other hand has been found to have a logarithmic dependence on density. However, other forms, Wigner type parametrized correlation energy functional being one of them, have also been applied in density functional calculations.
In order to solve for the density and therefrom the energy, one can take recourse to various approaches. One is the variational approach where one uses a parametric form of the trial density function and minimizes the energy functional with respect to variations in these parameters. The disadvantage of this approach is that the final form of the density and hence the shape of the radial density plot is determined apriori from the choice of
![]() (r) itself. However, the imposition of suitable constraints on the functional form of the density can help obtain the shell structure in atoms. In a different approach, Deb and Ghosh have treated the electron gas through its net density
(r) itself. However, the imposition of suitable constraints on the functional form of the density can help obtain the shell structure in atoms. In a different approach, Deb and Ghosh have treated the electron gas through its net density
![]() (r) without bothering about the individual electrons. They have started with a ``local" kinetic energy functional and translated the Euler equation into a single deterministic equation for the density. The solution of this equation for selected atomic systems does show shell structures in the radial density plots. The most well known approach for the determination of the density is however that of Kohn and Sham . They follow the footsteps of Hartree who considered a system of N non-interacting electrons in which each electron is assumed to move in an average field due to all other electrons and nuclei. Kohn and Sham opined that each electron moves under the influence of a local effective potential Veff, which includes, not only the exchange but also the correlation effects, viz.,
(r) without bothering about the individual electrons. They have started with a ``local" kinetic energy functional and translated the Euler equation into a single deterministic equation for the density. The solution of this equation for selected atomic systems does show shell structures in the radial density plots. The most well known approach for the determination of the density is however that of Kohn and Sham . They follow the footsteps of Hartree who considered a system of N non-interacting electrons in which each electron is assumed to move in an average field due to all other electrons and nuclei. Kohn and Sham opined that each electron moves under the influence of a local effective potential Veff, which includes, not only the exchange but also the correlation effects, viz.,
![]() or
or
![]()
The original Euler equation could then be written as
![]()
Using the condition
![]()
Kohn and Sham obtained the equation
![]()
They then concluded that for a given
Veff(r) one can obtain the density
![]() (r) which satisfies eqns. (1.1.16) and (1.1.17), simply by solving the one particle equations
(r) which satisfies eqns. (1.1.16) and (1.1.17), simply by solving the one particle equations
![]()

The Kohn-Sham orbitals ![]() and the corresponding eigen-values {
and the corresponding eigen-values {
![]() } do not have any strict physical meaning. They are suppositious entities resulting from a mathematical procedure. There is one exception though. The highest eigenvalue
} do not have any strict physical meaning. They are suppositious entities resulting from a mathematical procedure. There is one exception though. The highest eigenvalue
![]() is related to the chemical potential. All
is related to the chemical potential. All ![]() and {
and {
![]() }, however, have great semiquantitative importance, much like the Hartree-Fock wave functions and energies, often more so as they contain correlation effects and are consistent with the exact physical density. The solution of the Kohn-Sham equations thus leads one to calculate
}, however, have great semiquantitative importance, much like the Hartree-Fock wave functions and energies, often more so as they contain correlation effects and are consistent with the exact physical density. The solution of the Kohn-Sham equations thus leads one to calculate
![]() (
(![]() ), the ground state energy E, the kinetic energy T and other ground state properties that follow. The expressions for E and T are as follows, viz.,
), the ground state energy E, the kinetic energy T and other ground state properties that follow. The expressions for E and T are as follows, viz.,
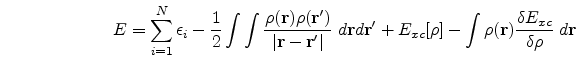
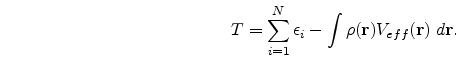
A beautiful review of density functional theory can be found in the book by Parr and Yang [1]. In conclusion, from the application point of view, DFT has proved its usefulness in the study of the physics of atoms, molecules and solids. Besides it has also been applied to problems of the nuclei as well as the liquid state. One of the first uses of DFT to study light atoms was made by Tong and Sham . Thereafter, others have used it to study light as well as heavy atoms. Open shell atoms have also been studied with the help of local spin DFT. Gunnarsson and his co-workers have pioneered the study of molecules using DFT. DFT has also been used extensively to solve problems involving the solid-state, the first work in this direction being that of Slater. Slater's
![]() -dependent exchange potential was also found to be dependent on a factor, `
-dependent exchange potential was also found to be dependent on a factor, `![]() ', which was allowed by him to vary somewhat from its value in the uniform electron gas. The method was christened the X
', which was allowed by him to vary somewhat from its value in the uniform electron gas. The method was christened the X![]() - method and involved the self-consistent solution of a series of one-electron equations. It may be pointed out that only because of the shortcomings in the Hartree-Fock method when dealing with solids did the X
- method and involved the self-consistent solution of a series of one-electron equations. It may be pointed out that only because of the shortcomings in the Hartree-Fock method when dealing with solids did the X![]() - method come into being. The HF method when applied to solids required a complicated superposition of deterministic wave functions and its results were often inaccurate. DFT on the other hand has been very successful in calculating the physical properties of solids, especially crystalline solids where there is a strong bonding between all the nearest neighbours. In such cases the entire crystal has to be thought of as a giant molecule. DFT has also been used to study very large molecules like proteins. It has also made forays into the domain of nuclear physics, having been used to calculate the bulk properties of nuclei as also the nuclear shell structure effects.
- method come into being. The HF method when applied to solids required a complicated superposition of deterministic wave functions and its results were often inaccurate. DFT on the other hand has been very successful in calculating the physical properties of solids, especially crystalline solids where there is a strong bonding between all the nearest neighbours. In such cases the entire crystal has to be thought of as a giant molecule. DFT has also been used to study very large molecules like proteins. It has also made forays into the domain of nuclear physics, having been used to calculate the bulk properties of nuclei as also the nuclear shell structure effects.