A primitive cell (sometimes called a primitive unit cell) is the smallest area cell (for a 2-dim lattice) or smallest volume cell (for a 3-dim lattice) which serves as the basic building block of the lattice. If we keep stacking the primitive cells without leaving any gap we would have obtained the lattice over all space. The primitive cell is mathematically obtained by the primitive translation vectors a, b and c, and for a three dimensional lattice its volume is given by |a . b x c|
In some situations symmetry dictates that we use another unit cell which is bigger than the primitive unit cell but which is simpler to work with. Such a unit cell is called a conventional unit cell. If we keep stacking the conventional unit cells without leaving any gap we would have obtained the lattice over all space, just as before.
Unlike a conventional unit cell, one can associate no more than one lattice point with a primitive unit cell.
Below is a java applet which shows different unit cells. Click on them to see which are conventional and which are primitive.
* Weigner-Seitz primitive cell
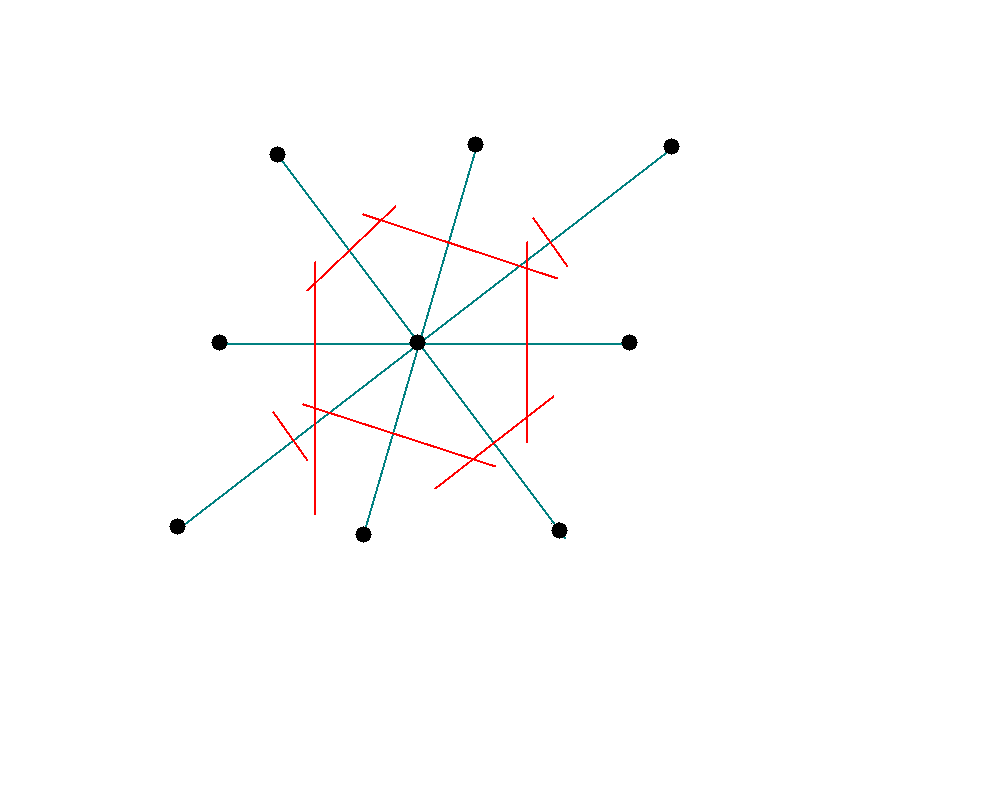
A primitive unit cell may also be constructed as follows:
(i) We start with an array of points in the (direct) lattice.
(ii) We connect any one lattice point to all the neighbouring lattice points with lines.
(iii) At the mid point of these lines we draw normals (if we started out with a two dimensional lattice) or normal-planes (if we started out with a three dimensional lattice). The smallest area (or volume) enclosed in this way is called the Wigner-Seitz primitive cell of the direct lattice. All space may be filled up without leaving any gap by joining these Wigner seitz primitive cells.
