A crystal may be thought of as being made up of many different sets of parallel and equidistant planes passing through the lattice points. These are called lattice planes. Many properties of the crystal can be understood in terms of the spatial geometry of these planes. Miller indices (hkl ) is a set of three numbers h,k,l used to designate these different sets of planes.
How to obtain the Miller indices?
Any plane in the crystal can be thought of as making intercepts on the crystallographic axes a, b and c which may be primitive or non-primitive.
Express the intercepts in terms of multiples of unit lattice constants (a,b,c).
Find the reciprocal of the numbers.
Reduce the reciprocals to smallest integers by multiplying them with the least common multiple of their denominators. Enclose the integers in a parentheses: (hkl).

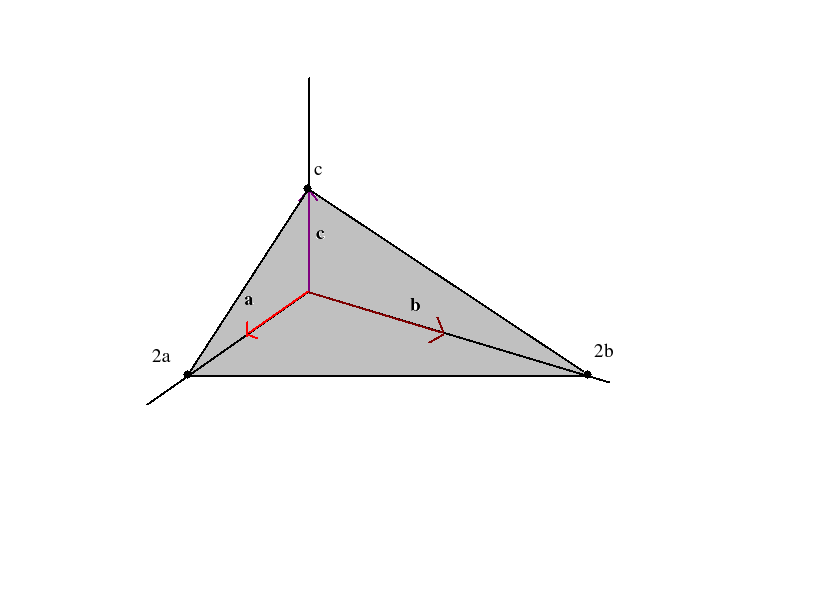
The plane in the figure makes intercepts 2a, 2b and c. So we consider the set of numbers 2,2,1.
Their reciprocals are 1/2, 1/2 and 1.
Express them as the smallest set of integers by multiplying each with the LCM of their denominators,viz.,2
So we have the miller indices for the plane as (hkl )= (112)
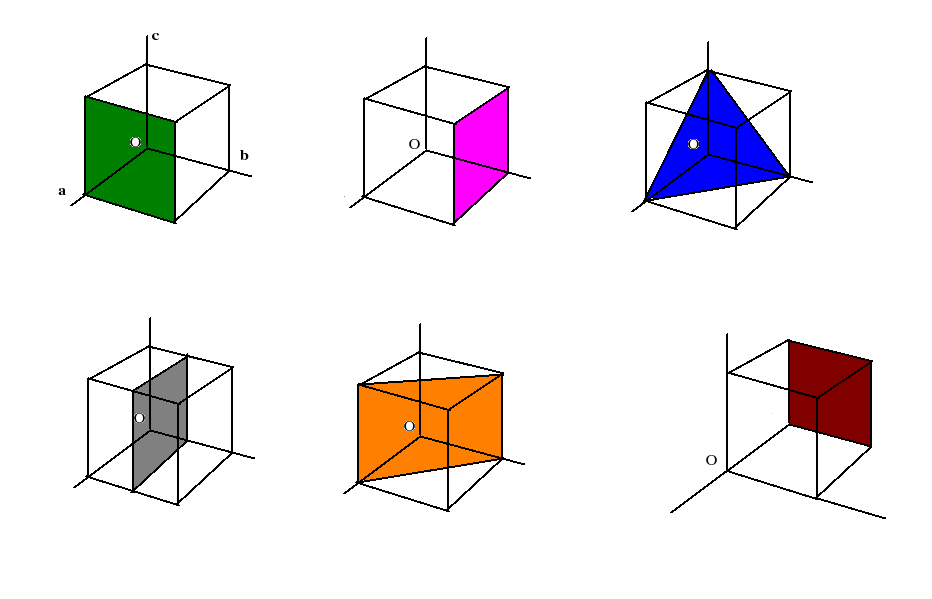
Below we have shown different planes in a cubic crystal. Obtain their miller indices.