The cubic family of lattices comprising of simple, body-centered and face-centered varieties and the hexagonal closed packed (hcp) lattice are the most important.
Some crystallographic terms we frequently encounter are as follows:
*Nearest neighbour spacing: The distance between the center of an atom from the center of another atom which is closest to it.
*Coordination number: The number of neighbouring atoms to any one atom which are closest to it.
*Packing fraction: The ratio of the volume of atoms associated with a unit cell to the volume of the unit cell itself.
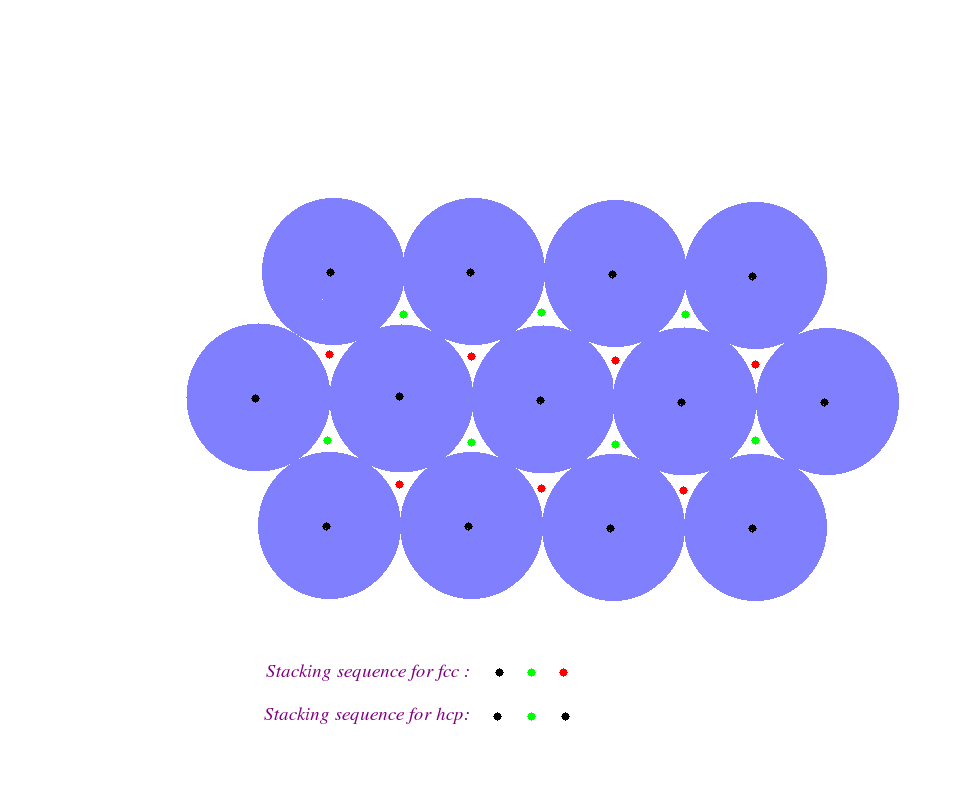
hcp is one of the two most closely packed crystal structure, the other being face centred cubic or fcc structure. See the figure below closely to understand the difference between the two structures.

It gives us a top view of two crystal structures. The violet coloured spheres represent the closely packed atoms belonging to a particular planar layer in three dimensional space. The atoms of this layer are designated by the black dots at their centres. There is another layer of identical atoms stacked above this layer. These atoms, in order to form a closely packed structure, lie in the wedges marked with the green dots. Let these atoms be designated by the green dots.
The difference in the fcc and hcp structures lies in the stacking of atoms in the layer on top of the previous layer. If the next layer of atoms lie in the wedges marked with red dots then the structure is an fcc one. On the other hand if the next layer of atoms lie in the wedges which are created atop the center of the atoms of the original layer and which were marked with black dots, then the structure is an hcp one.
Let us dwell on the hcp lattice. The following figure shows a conventional unit cell of the hcp crystal structure. Note the position of atoms at the corners of the hexagonal planes which are stacked one upon other.
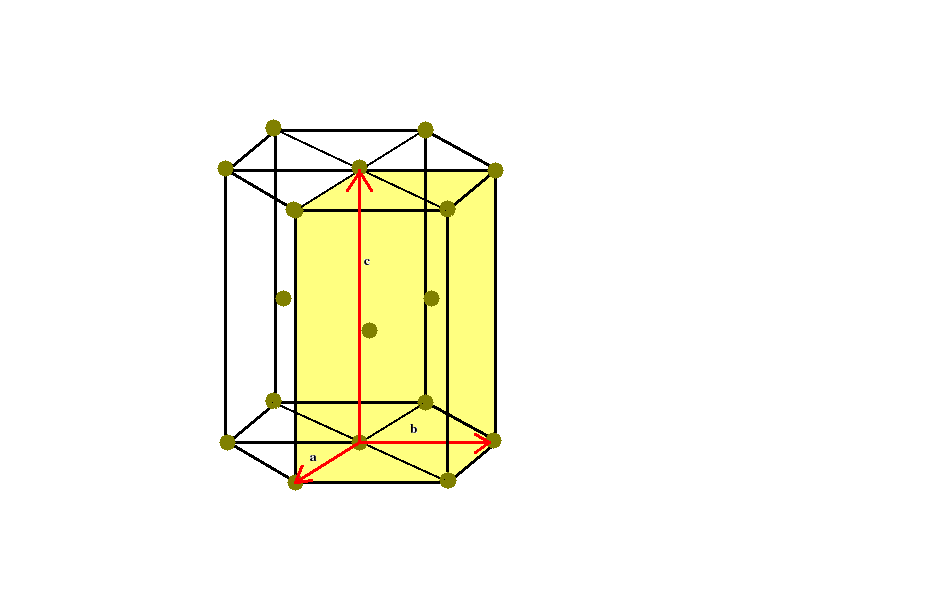
Note also the three primitive translation vectors a,b,c, which define the primitive unit cell (the rectangular parallelepiped coloured in yellow).
In order to understand the stacking of atoms in the layers from a three dimensional perspective lets have a detailed look at the figure below.
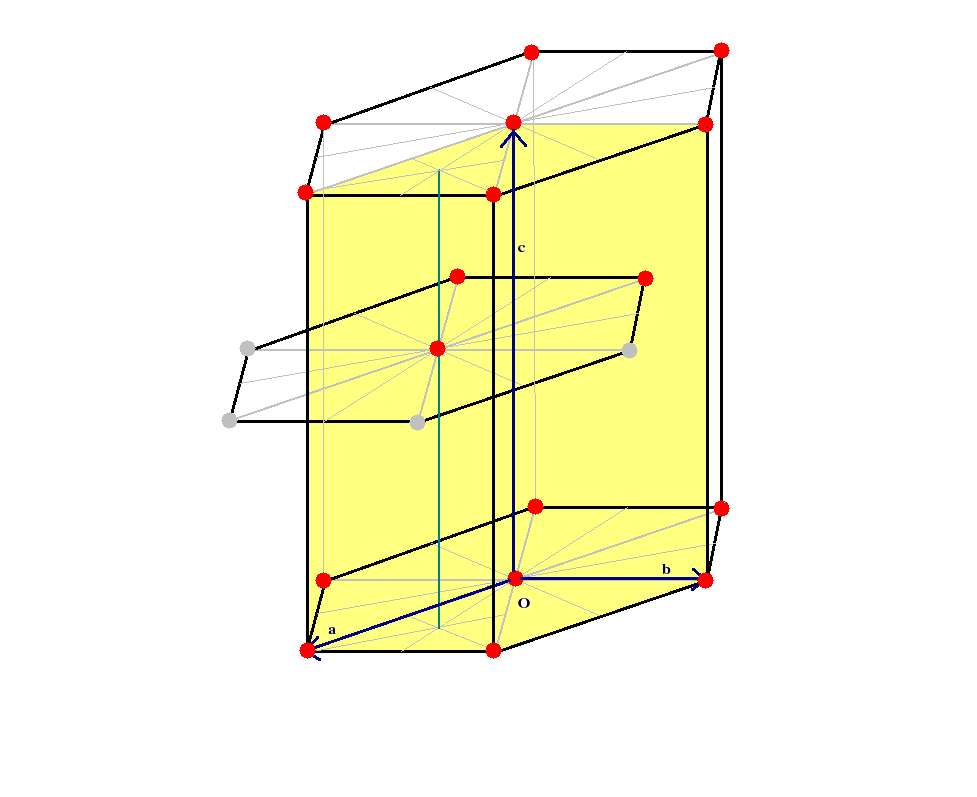
The following points may be noted from the figure.
* The middle layer of atoms is slightly shifted vis-a-vis the bottom and top layers which are exactly aligned vertically. Hence three of the atoms of the middle layer lie inside the unit cell and three lie outside.
*The atom at the middle of planar hexagon for the middle layer lies on top of the centroid of the equilateral triangle lying beneath on the bottom layer.
* The top layer shares six corner atoms and one central atom with the conventional unit cell. So does the bottom layer. Note however that each corner atom is shared by six unit cells, as is evident from the figure for the unit cell. So each corner atom contributes 1/6th of itself to the conventional unit cell. Similarly each face centred atom is shared by two unit cells (one above and one below). Hence each such atom contributes 1/2 of itself to the conventional unit cell.
* Finally the three atoms of the middle layer lie wholly inside the conventional unit cell, so their contribution is whole. So in all the number of atoms that can be associated with one conventional hcp unit cell is 12 x (1/6) + 2 x (1/2) + 3 = 6.
In order to find the coordination number, we note that the face centred atom in the top layer just touches the six other atoms at the face corners of the same layer. It also touches the three atoms of the middle layer. By symmetry it should also touch the three atoms of the next layer above its own layer. hence in all it just touches twelve other atoms. Therefore its coordination number is 12.
Lets now to refer to the figure below and calculate the
![]() ratio of the hcp structure.
ratio of the hcp structure.
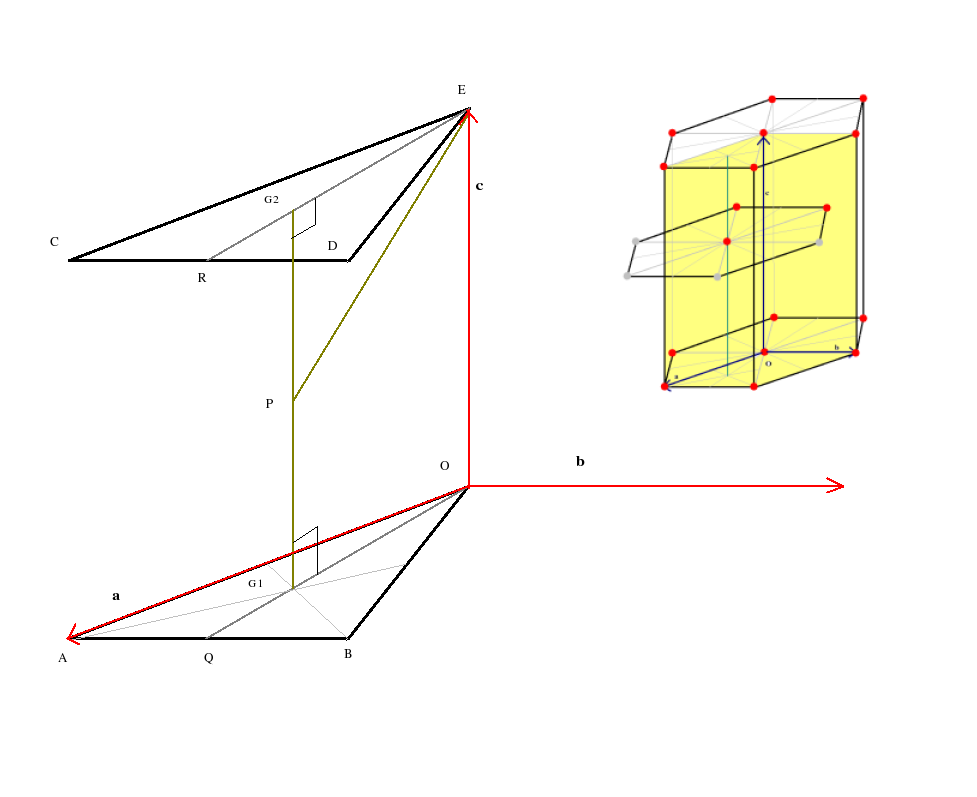
The atom at E touches the corner atoms C and D in its own layer as also the atom P in the layer beneath. Also ECD is an equilateral triangle; so the atoms at C and D also touch each other. Therefore PE = CD = ED = 2r where r is the radius of each atom.Now CD = a where a is the one of the lattice constants of the lattice (the other lattice contant being c). So 2r = a
ER is the median of the equilateral triangle ECD. Therefore
ER = EDCos30 = acos(30) or
EG2 = (2/3)ER or
EG2 = ![]() .
.
G2 is the centroid of the equilateral triangle ECD.
PG2 = (1/2)G1G2 = ![]() Therefore in right angled triangle EPG2
EP2 = PG22 + EG22 or
(2r)2 = (
Therefore in right angled triangle EPG2
EP2 = PG22 + EG22 or
(2r)2 = (![]() )2 + (
)2 + (![]() )2.
)2.
Hence we have
![]() = 1.633
= 1.633
Finally we shall calculate the packing fraction.
Volume of each atom of the structure equals
(4/3)![]() r3. We already know that for hcp structure 2r = a. Moreover as we have already discussed, 6 atoms may be associated with one conventional hcp unit cell.
Volume of one unit cell is
a . b x c or
a2 x c which is readily found out using the
r3. We already know that for hcp structure 2r = a. Moreover as we have already discussed, 6 atoms may be associated with one conventional hcp unit cell.
Volume of one unit cell is
a . b x c or
a2 x c which is readily found out using the
![]() ratio obtained earlier.
ratio obtained earlier.
With this information we can then obtain the packing fraction of an hcp structure as 0.74. If we had done a similar analysis of the fcc structure we would have found that the packing fraction of fcc structure is also 0.74. Why not do it yourself.