Reciprocal Lattice

* Every crystal has two types of lattices (i) A direct lattice and (ii) A Reciprocal Lattice. The is a microscopic image of the crystal and the reciprocal lattice is an x-ray diffraction pattern of the crystal.

* Just as the direct lattice is defined by the direct lattice translation vector:

$$\begin{eqnarray*} \mathbf{T} & = & u\mathbf{a}+v\mathbf{b}+ w\mathbf{c} \end{eqnarray*}$$

a, b, c being the primitive vectors of the direct lattice and u, v, w being integers, the reciprocal lattice is defined by the reciprocal lattice vector:

$$\begin{eqnarray*} {\mathbf {\sigma}_{hkl}} \;=\; \mathbf{G} & = & h\mathbf{A} + k\mathbf{B} + l\mathbf{C} \end{eqnarray*}$$

A, B, C being the primitive vectors of the reciprocal lattice and h, k, l being integers.

The two sets of lattices are related as follows:

$$\begin{eqnarray*} \mathbf {A} & = & 2\pi \frac{\mathbf{b}\times\mathbf{c}} {\mathbf{a}\bullet{\mathbf{b}\times\mathbf{c}} \end{eqnarray*}$$

$$\begin{eqnarray*} \mathbf {B} & = & 2\pi \frac{\mathbf{c}\times\mathbf{a}} {\mathbf{a}\bullet\mathbf{b}\times\mathbf{c}} \end{eqnarray*}$$

$$\begin{eqnarray*} \mathbf {C} & = & 2\pi \frac{\mathbf{a}\times\mathbf{b}} {\mathbf{a}\bullet\mathbf{b}\times\mathbf{c}} \end{eqnarray*}$$

Now lets ponder for a while why at all we need something like a reciprocal lattice? When we deal with crystals, we should know that their physical properties quite often depends on particular directions inside the crystal: we then say that the crystal is anisotropic. This anisotropy can be explained by the fact that inside the crystal there are many sets of parallel planes which are oriented in different directions. Interestingly the normal to these planes represent the same directions as do the planes. However, while these planes are two-dimensional, their normals are one-dimensional. Hence it would be much simpler if we used the normals to study the crystal.

Besides, when we study X-ray diffraction in a crystal we would see that x-rays of a particular wavelength and particular glancing angle would be diffracted from only a particular set of planes (hkl) having a fixed interplanar spacing.

Keeping the above points in mind we may proceed to construct a reciprocal lattice from a direct lattice.

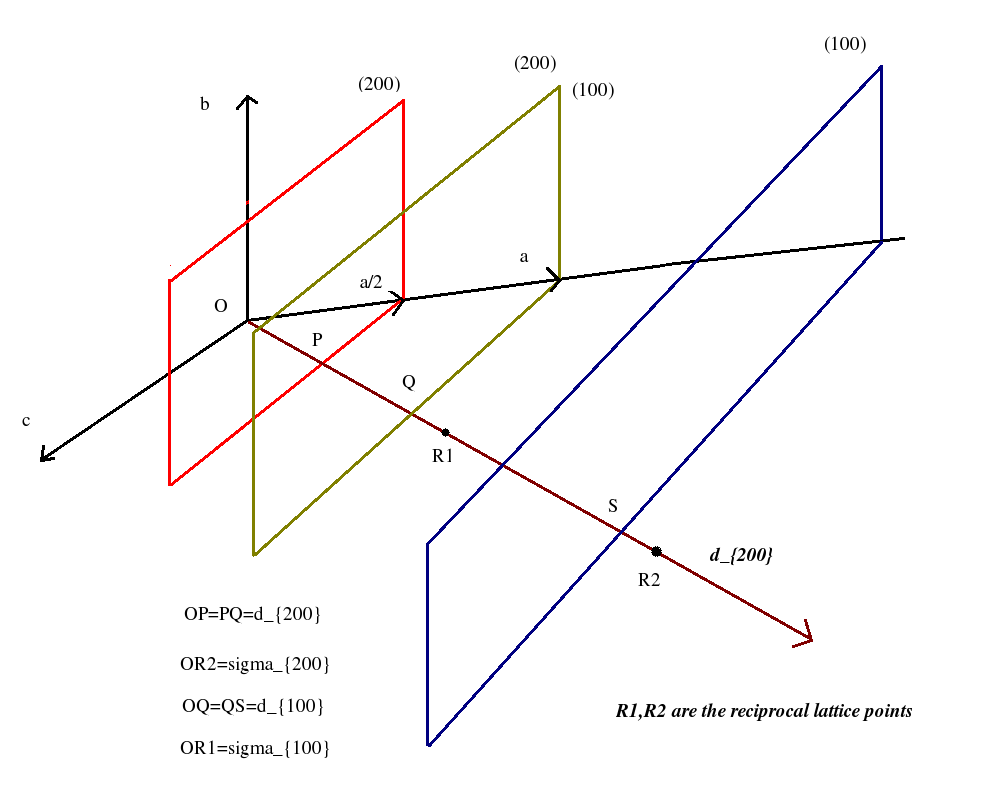
(i) We start from a point on the direct lattice space, call it the origin (O) and draw the three basis (primitive) vectors a,b,c.Click here to see

(ii) Draw the set of two parallel (100) planes and draw the common normal to the planes. Lets call the interplanar spacing OQ = QS = d₁₀₀. Locate a point R₁ on the normal so that $\sigma_{{100}}^{}$ = OR₁ = K x (1/d₁₀₀), K is a constant. Click here to see

(iii) Draw another set of two parallel (200) planes and draw the common normal to the planes. This normal would coincide with the one to the (100) planes obtained above. We must remember that the interplanar spacing OP = PQ = d₂₀₀ would be half of d₁₀₀. Now we locate a point R₂ on the common normal so that $\sigma_{{200}}^{}$ = OR₂ = K x (1/d₂₀₀), K being the same constant as above.Note that $\sigma_{{200}}^{}$ = 2 x $\sigma_{{100}}^{}$. Click here to see

(iv) We would thus have obtained two points of the reciprocal lattice (viz., R₁ and R₂), corresponding to the two sets of planes (100) and (200) respectively. For all the (h00) planes in the direct lattice, we can similarly obtain the corresponding reciprocal lattice points. The spatial period in the reciprocal lattice is therefore given by A = $\sigma_{{100}}^{}$ = K x (1/d₁₀₀). A is therefore the primitive or basis vector of the reciprocal lattice along the normal to the b- c plane of the direct lattice. By similar reasoning we could obtain the two other basis vectors , viz., B = $\sigma_{{010}}^{}$ = K x (1/d₀₁₀) and C = $\sigma_{{001}}^{}$ = K x (1/d₀₀₁) along the normals to the c- a and a- b planes respectively. Click here to see