Theory of frequency modulation and phase modulation
In frequency modulation scheme, the frequency of the carrier signal is modulated or changed in accordance with the instanteneous value of the information carrying modulating signal. In phase modulation, on the other hand, it is the phase angle of the carrier signal which is modulated in accordance with the instanteneous value ofthe modulating signal.
The carrier signal
We start with a sinusoidally varying signal called the 'carrier', usually of high frequency, and expressed as
< br />
The modulating signal
Next we consider the message signal containing the information to be transmitted. This signal is called the modulating signal as it is used to modulate or change some charecteristic of the carrier signal. It is of lower frequency vis-a-vis the carrier. The modulating signal may have different forms. We consider here a cosinusoidal modulating signal expressed as
The Frequency-Modulated (FM) signal
In order to obtain an expression for the frequency-modulated signal, we start with the instanteneous value of the modulated frequency of the carrier, ![]() , keeping in mind that in frequency modulation the carrier frequency is modulated by the instanteneous value of the modulating signal. By instanteneous, we mean, that which changes with time. The relevant expression would then be:
, keeping in mind that in frequency modulation the carrier frequency is modulated by the instanteneous value of the modulating signal. By instanteneous, we mean, that which changes with time. The relevant expression would then be:
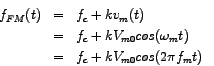
Since the amplitude of the carrier remains fixed in frequency modulation, the form of the instanteneous frequency-modulated signal would be:
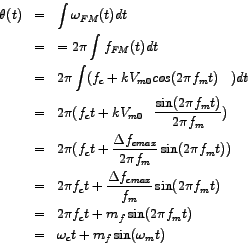
Side-frequency components of the FM signal
A look at the expression for the frequency-modulated wave, viz.,
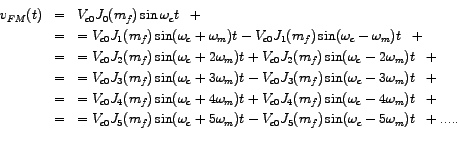
The values of the Bessel-functions can be obtained from tabulated values and graphs for different values of the modulation-index
From the expression above we observe that the FM wave comprises of a modulated carrier component of frequency
We thus observe that the frequency-components add up to generate the frequency-modulated (FM) waveform. The amplitude of the modulated carrier component is decreased from that of the unmodulated carrier but the decrease is fully compensated by contributions from other side-frequency components. As a result, the amplitude of the FM wave equals that of the unmodulated carrier.
The Frequency-Spectrum
The frequency components in a frequency-modulated wave are expressed as vertical lines spaced ![]() apart on both sides of the carrier frequency
apart on both sides of the carrier frequency ![]() in what is called a frequency-spectrum of the FM wave or the FM spectrogram.
in what is called a frequency-spectrum of the FM wave or the FM spectrogram.
The height of each line is proportional to the amplitude of the respective component. The central line depicts the spectral component at the carrier frequency which we call the modulated carrier component. The lines on both sides represent the odd-order and even-order side-frequency component pairs. Each pair of such components is depicted with a line of unique colour in the spectrograms in our right-hand panel. Recall from the expression of the FM wave in terms of its side-frequency components, that the lower frequency component of each odd-order side-frequency pair is always subtracted from the upper frequency component of that pair. On the other hand the lower frequency component of each even-order side-frequency pair is always added from the upper frequency component. This phase relationship between the side-frequency components is expressed in the line spectrum (the first spectrogram in the right-hand panel) by inverting all lines that correspond to the lower frequency componenents of the odd-order frequency component pairs.
However, in a conventional FM spectrogram as shown in the second spectrogram, all the lines are always on the +ve side, since the phase behaviour is considered to be of not much practical importance.
The band-width occupied by the spectrum is given by
![]() . Now one observation that comes out very clearly from the spectrgram plots is that the higher-order side-frequency components in general are of reduced amplitude. Taking this into consideration, Carson derived a formula for the band-width by considering only those frequency component pairs that together contribute 96 % of the total radiated power (power is proportional to square of amplitude) which is given below:
. Now one observation that comes out very clearly from the spectrgram plots is that the higher-order side-frequency components in general are of reduced amplitude. Taking this into consideration, Carson derived a formula for the band-width by considering only those frequency component pairs that together contribute 96 % of the total radiated power (power is proportional to square of amplitude) which is given below:
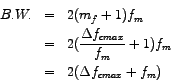
It is also interesting to observe how the spectrograms behave when the modulation-index
Phase-Modulation (PM)
In phase modulation, as stated at the outset, the instanteneous phase of the carrier is modulated in accordance with the instanteneous value of the modulating signal. The carrier frequency remains constant. We express this mathematically by writing the phase-modulated (PM) carrier as
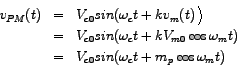
Here
Interestingly, the above expression for
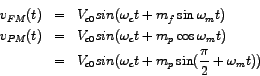
We must bear in mind that the analysis above pertains to the simple case of tone-modulation (the modulating signal being a sinusoidal one of single frequency). An analysis for the general case throws up some important conclusions regarding the similarity and difference between FM and PM. A general carrier signal is represented by
In phase-modulation,
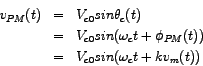
Now, the instanteneous frequency of rotation of the carrier-phasor is given by
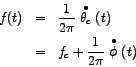
For phase modulation (PM), this reduces to:
For frequency-modulation (FM), on the other hand, we have already seen that the instanteneous frequency is given by:
Comparing the above equation with the general expression for instanteneous frequency (
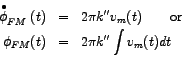
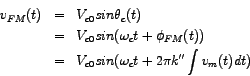
So what may we conclude from the above analysis?
1. Frequency and phase modulation are essentially similar to each other.
2. By integrating the modulating or message signal and passing the result through a phase-modulator, we can obtain a frequency-modulated (FM) signal.
3. Conversely, by differentiating the modulating or message signal and passing the result through a frequency-modulator, we can obtain a phase-modulated (PM) signal.
4. FM and PM, both have time-varying i.e. instanteneous phase and frequency. The forms are however different. In fact the nomenclature 'angle-modulation' was coined to mean either of the two.
© Abhijit Poddar All rights reserved.