
What is a lattice?
A lattice is a hypothetical regular and periodic arrangement of points in space. It is used to describe the structure of a crystal. Lets see how a two-dimensional lattice may look.

A basis is a collection of atoms in particular fixed arrangement in space. We could have a basis of a single atom as well as a basis of a complicated but fixed arrangement of hundreds of atoms. Below we see a basis of two atoms inclined at a fixed angle in a plane.

Let us now attach the above basis to each lattice point (in black) as follows.

Next remove the lattice points in black (remember that the lattice is an abstract entity). Lets see what we have got?

We have got the actual two-dimensional crystal in real space. So we may write:
lattice + basis = crystal
How do we define a lattice mathematically?
If r be the coordinates of a lattice point from any origin, then if we apply a lattice translation thought the lattice translation vector
![]()
then we would arrive at any other lattice point
r![]() around which the environment would look exactly the same as around
r.
around which the environment would look exactly the same as around
r.
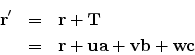
a, b and c are the primitive translation vectors or basis vectors which form the primitive cell of the lattice and u, v, w are integers.