What is a wave packet?
In quantum mechanics the motion of a particle is represented by that of a wave packet. The wave packet is a wavefunction
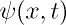 obtained
by superposing many harmonic (sine, cosine) or equivalently exp(ikx) wavefunctions
corresponding to different linear momenta
obtained
by superposing many harmonic (sine, cosine) or equivalently exp(ikx) wavefunctions
corresponding to different linear momenta
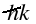 . The larger the number
of wave functions in the superposition, the more localized the wave
packet is in space and the corresponding particle can be measured more
precisely. Simultaneously the measurement of the momentum of the
particle becomes more imprecise. This is in
accordance with Heisenberg's uncertainty principle.
. The larger the number
of wave functions in the superposition, the more localized the wave
packet is in space and the corresponding particle can be measured more
precisely. Simultaneously the measurement of the momentum of the
particle becomes more imprecise. This is in
accordance with Heisenberg's uncertainty principle.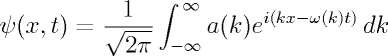
The
coefficients (a(k)) are
obtained by taking the inverse Fourier transform of the superposed wave
function at t=0 as follows:
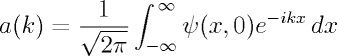
The wave function
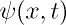 is the most
general solution of the time dependent Schrodinger equation for a free
particle. The w-k relationship
for such a particle obtained from the the deBroglie relations is found
to be non-linear.
is the most
general solution of the time dependent Schrodinger equation for a free
particle. The w-k relationship
for such a particle obtained from the the deBroglie relations is found
to be non-linear. 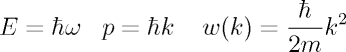
Hence the wave packet for the free
particle moving in such a dispersive medium would get temporally
dispersed or distorted while evolving with time with a group
velocity 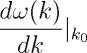 .
k is centred about k_{0}
and is assumed to vary little. It bears mention that an electromagnetic
wave travelling in free space corresponds to a non-dispersive medium as
the w-k relationship is linear
.
k is centred about k_{0}
and is assumed to vary little. It bears mention that an electromagnetic
wave travelling in free space corresponds to a non-dispersive medium as
the w-k relationship is linear 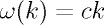 c being the speed of light which is
constant. The wave packet then travels undistorted with constant
speed c.
c being the speed of light which is
constant. The wave packet then travels undistorted with constant
speed c.
Simulation of a wave packet striking a potential barrier
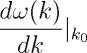 .
k is centred about k_{0}
and is assumed to vary little. It bears mention that an electromagnetic
wave travelling in free space corresponds to a non-dispersive medium as
the w-k relationship is linear
.
k is centred about k_{0}
and is assumed to vary little. It bears mention that an electromagnetic
wave travelling in free space corresponds to a non-dispersive medium as
the w-k relationship is linear 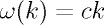 c being the speed of light which is
constant. The wave packet then travels undistorted with constant
speed c.
c being the speed of light which is
constant. The wave packet then travels undistorted with constant
speed c. Simulation of a wave packet striking a potential barrier
Now we consider what happens when a
particle encounters a rectangular potential barrier of infinite height
and finite width. If the particle behaves classically, there is no way
it can go over to the other side of the barrier. However, from a quantum mechanical perspective, the particle
can be represented as a wave packet and the wave packet can be shown to
penetrate or tunnel through the barrier. Below is presented a
simulation which makes it more understandable.
To obtain the simulation, one needs to solve Schrodinger's time dependent equation for the rectangular barrier potential. The solution may be launched with a Gaussian wave packet and the modulus of the wave function representing the wave packet is to be plotted at fixed intervals of time. Finally the plots are to be animated with the help of an image manipulation program like photoshop or gimp.
To obtain the simulation, one needs to solve Schrodinger's time dependent equation for the rectangular barrier potential. The solution may be launched with a Gaussian wave packet and the modulus of the wave function representing the wave packet is to be plotted at fixed intervals of time. Finally the plots are to be animated with the help of an image manipulation program like photoshop or gimp.
Hey, do you notice that along with
the transmitted wave there are also a few reflected components?
Do you want to create such a simulation yourself? Refer to Goldberg et al.'s paper (Am. J. Phys., 35, 177 (1967)).
Do you want to create such a simulation yourself? Refer to Goldberg et al.'s paper (Am. J. Phys., 35, 177 (1967)).