Signals and Systems

A signal may be thought of as an electrical waveform which is to be communicated or transmitted over a distance. Any message or data which is non-electrical in form, like human voice, television picture etc. needs to be first converted by a transducer to an electrical signal.

Continuous and discrete time signals

Analog signals refer to continuous signals in the form of message or data whose values change continuously with time.
Examples:
* human voice or more specifically acoustic pressure changes when we speak
* temperature at a particular location
etc.

Digital signals are discrete-time signals and refer to message or data whose values are discrete and do not change continuously with time.
Examples:
* Printed text is a digital message
* Morse coded telegraph message

A Deterministic signal is one which has no uncertainty or randomness and can be expressed by a mathematical function of time.
Examples: A sine wave signal or a square wave signal

A Non-Deterministic signal is one whose value is uncertain or random at different instants of time. It cannot be expressed by a mathematical function. It is studied with the help of statistics.
Example: A noise signal

A Periodic signal is one which repeats after a given period of time. It can be expressed mathematically by a function \(f(t)\) as:
\( f(t) = f(t+T) \quad \ldots (1) \quad \) where \(T\) is called the time-period.
Example: See figure below

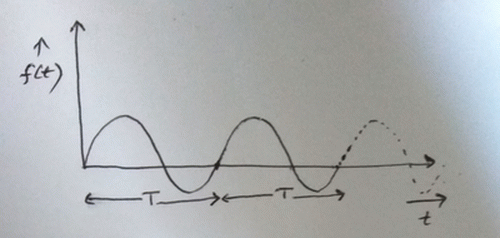
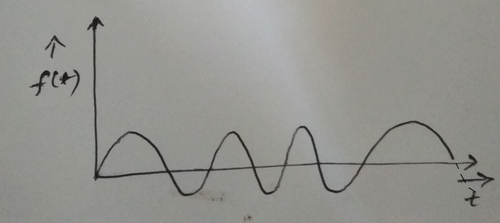
An Aperiodic signal is one which has no periodicity. It does not repeat after a period of time.
Example: See figure below

Symmetric signal: A signal whose time-reversed form is equal to the signal itself. It is also called an even-signal.
\( f(t) = f(- t) \quad \ldots (2) \quad \)
Example: A Cosine wave signal

Anti-Symmetric signal: A signal whose time-reversed form is equal to the negative of the signal itself. It is also called an odd-signal.
\( f(t) = - f(- t) \quad \ldots (3) \quad \)
Example: A Sine wave signal

Signal Energy: If the signal is represented by the function \(f(t)\), then its energy \(E\) is defined mathematically as:
\( \displaystyle{E = \int_{-\infty}^{+\infty} f^{2}(t) dt \qquad\qquad ....\;(4) } \)

Signal Power: If the signal is represented by the function \(f(t)\), then its power \(P\) is defined mathematically as:
\( \displaystyle{P = \lim_{T\to \infty} \frac{1}{T} \int_{-\frac{T}{2}}^{+\frac{T}{2}} f^{2}(t) dt \qquad\qquad ....\;(5) } \)

Note that \(E\) is not the actual energy of the signal. It can instead be thought of as the energy dissipated in a load resistor \(R\) = 1 ohm if a voltage \(f(t)\) were applied across \(R\). This follows from eqn. 4.
In all of the above, the signal is considered to be real. If it is complex, then we must use \(\vert f(t) \vert ^2\) instead of \( f^2(t) \).

A Causal signal is defined by a function \(f(t)\) as:
\( \displaystyle{ f(t) = 0 \quad }\) for \( \quad t \lt 0 \qquad\qquad ....\;(6)\)
It implies that the signal starts at \(t=0\) or after.
For e.g. A unit step function: \(f(t) = u(t) \quad \ldots \; (7) \)

An Anti-Causal signal is defined by a function \(f(t)\) as:
\( \displaystyle{ f(t) = 0 \quad }\) for \( \quad t \gt 0 \qquad\qquad ....\;(8)\)
For e.g. \(f(t) = -u(t) \quad \ldots \; (9) \)

A Non-Causal signal is defined by a function \(f(t)\) as:
\( \displaystyle{ f(t) \neq 0 \quad }\) for \( \quad t \gt 0 \qquad\qquad ....\;(10)\)
For e.g. \(f(t) = u(t+1) \quad \ldots \; (11) \)

In all of the above \(u(t)\) is the unit step function
\( \displaystyle{ \begin{split} u(t) & = & 1 & \quad for \quad & t \geq 0 \\ & = & 0 & \quad for \quad & t \lt 0 \qquad \ldots\; (12) \end{split} }\)

Working with signals in the time-domain refers to studying how the signal changes with time. When talking of frequency-domain, we refer to the behaviour of the signal within a range of its frequency components. This is also referred to as the frequency-spectrum. In Digital Signal Processing (DSP) , we also come across the term spatial-domain. This referes to the spatial location of the pixels constituting the digital image which is being processed.

Time and frequency domain signals may be considered as one-dimensional signals where as spatial domain signals may be thought of multi-dimensional signals.

We may move from one domain to another by transformation of the independent variables, time, frequency and space. For example, one may use Fourier transform to convert a signal from the time domain to its frequency domain and use an inverse-Fourier transform to go back to the time-domain.

The periodic sinusoidal signal can be expressed as a sine function of the form:
\( \displaystyle{ f(t) = A sin (\omega t + \phi) \qquad\qquad \ldots\;(13) }\)

The aperiodic exponential signal can be expressed as an exponential function of the form:
\( \displaystyle{ f(t) = A e^{m t} \qquad\qquad \ldots\;(14) }\)
For a real exponential signal, \(A\) and \(m\) are real. We may also deal with complex exponential signals for which both \(A\) and \(m\) are complex.

The unit step function (\(u(t)\)), already been defined in eqn. 12, is repeated below:
\( \displaystyle{ \begin{split} u(t) & = & 1 & \quad for \quad & t \geq 0 \\ & = & 0 & \quad for \quad & t \lt 0 \qquad \ldots\; (12) \end{split} }\)
See figure below:

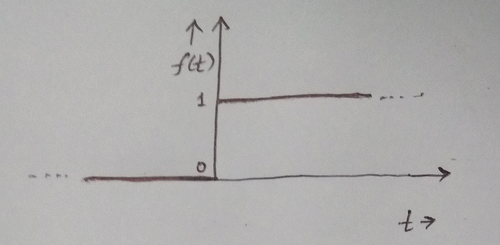
The unit impulse function (\(\delta(t)\)), also called the delta-function, is defined as:
\( \displaystyle{ \begin{split} \delta (t) & = & 0 & \quad for \quad t \neq 0 & \\ \int_{-\infty}^{+\infty} \delta (t) dt & = & 1 & & \qquad \ldots\; (15) \end{split} }\)
See figure below:

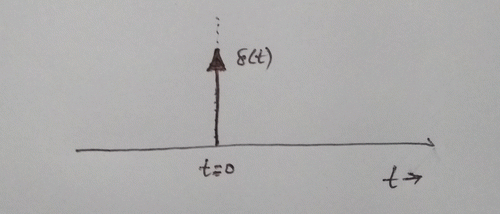
It is important to note that the unit impulse function is undefined at \(t=0\), yet satisfies eqn. 15.

A System refers to an entity that transforms input signals to output signals. Mathematically it may be thought as a function which maps input signals to output signals.
A discrete time system refers to a system where the input and output signals are discrete in time. On the other hand, a continuous time system refers to a system where the input and output signals are continuous in time.
Systems may be further classified as:

Static (memoryless) and Dynamic (with memory) Systems
Linear and Non-linear Systems
Time Variant and Time Invariant Systems
Stable and Unstable Systems
Causal and Non-causal Systems
Invertible and Non-Invertible Systems

Based on the above, a few important system properties are discussed below in brief:

A System without memory (Memoryless system) is one where the output at time \(t\) depends only on the present input at time \(t\). For e.g. An ideal amplifier. A System with memory, on the other hand, is one where the output at time \(t\) depends on the past or future inputs ( at time \(\lt t \) \(\,\) or \(\,\) \(\gt t \) ). For e.g. a system comprising of reactive elements (capacitors and inductors) which can store energy is said to have memory.

A Linear system is one for which the following two properties of linearity, namely homogeneity and superposition, are satisfied. Otherwise, the system may be said to be Non-linear.
Homogeneity:
\( \displaystyle{ B(a x) = a B(x) \qquad\qquad \ldots\; (16) }\)
Superposition:
\( \displaystyle{ B(x_1 + x_2) = B(x_1) + B(x_2) \qquad\qquad \ldots\; (17) }\)
where \(B\) represents the system, \(x, x_1, x_2\) are the inputs and \(a\) is a constant.
Integrators and differentiators are examples of linear systems. A comparator circuit is a non-linear system.

A Time-invariant system is one where if the input is shifted in time by say \(\tau\), then the output is also shifted by the same time \(\tau\), otherwise it is referred to as a Time-variant system. If the system be mathematically represented by a function \(B\), and \(x\) and \(y\) be the input and output respectively, then time-invariance implies:
\( \displaystyle{ \begin{split} y(t) & = & B x(t) & \qquad\qquad \ldots\; (18)\\ y(t - \tau) & = & B x(t - \tau) & \qquad\qquad \ldots\; (19)\\ \end{split} }\)
A simple \(R\)-\(C\) circuit (\(R, C\) and an a.c. source connected in series) is a time-invariant system as long as the values of \(R\) and \(C\) do not change.

A system is said to possess stability or is called a Stable system if a bounded input signal always results in a bounded output (BIBO) signal. Otherwise it may be characterized as an Unstable system.
A signal \(x(t)\) is said to be bounded if:
\( \displaystyle{ \vert x(t) \vert \leq M \qquad\qquad \ldots\; (20) }\)
where \(M\) is a +ve number \( \lt \infty \).
For e.g. a system represented by the equation \(y(t)=sin(x(t))\) is stable whereas the system described by the equation \(y(t) = \frac {x(t)}{sin(t)} \) is unstable.

A system is called a Causal system or said to possess causality if the output at any time \(t\) depends on the input at time \(t\) or before \(t\) and does not depend on the input at a future time after \(t\). If the output depends also on the input at a future time, then it is said to be Non-causal.
\( \displaystyle{ \begin{split} y(t) & = & x(t) + x(t-1) & \qquad\qquad \ldots\; (21)\\ y(t) & = & x(t) + x(t+1) & \qquad\qquad \ldots\; (22)\\ \end{split} }\)
In the above, eqn. 21 represents a causal system where as eqn. 22 represents a Non-causal system. Can you explain why?

Invertibility in a system points to the situation where the input signal appears at the output. The system is then said to be an Invertible system for which:

\( \displaystyle{ y(t) = x(t) \qquad\qquad \ldots\; (23) }\)
Otherwise it is a Non-invertible system.

The write-up above has been deliberately kept brief, keeping in view the need of the students in the present uncertain times. For detailed understanding, students are advised to refer to their text books or the web-links below

Signal Classifications and Properties by Melissa Selik et al

Signals and systems: Prof. Paul Cuff

Signals and systems continued: Prof. Paul Cuff

Systems classification: tutorialspoint

BEC 301 Signals and systems

To be continued \( \ldots \)
Dr. Abhijit Poddar