Suplementary notes on select topics in physics and electronics
Standing waves in a transmission line New

Operating modes of 8255A PPI New

Select theory of pn junction diode

Resonance in series LCR circuit

Wave packet and its dynamics

Theory of frequency modulation





Go back to main teaching page


Standing waves and Standing wave patterns in transmission lines
Abhijit Poddar
www.abhipod.com

Standing waves are created by the superposition of incident and reflected travelling waves in an improperly terminated transmission line. By improper termination, what is meant is, the load impedance has a value different from that of the characteristic impedance of the line.

Experience tells us that the teaching and learning of standing waves and standing wave patterns in differently terminated transmission lines can be best accomplished with the aid of animations. Below, I have embedded YouTube videos of animations related to the generation of standing waves and standing wave patterns. The animations have been created by myself, invoking Gnuplot iteratively through a shell script, to read and plot the data generated from simple Fortran programs. Although some Fortran compilers permit invoking of Gnuplot from inside the program itself and the plot of data on the fly, I chose the easier process outlined above.

To learn more about the theory behind standing waves, you need to scroll down this page.

Animation Videos on Standing Waves and Standing Wave Patterns in Transmission Lines





Formation of Standing Wave Patterns in a Lossy Transmission Line




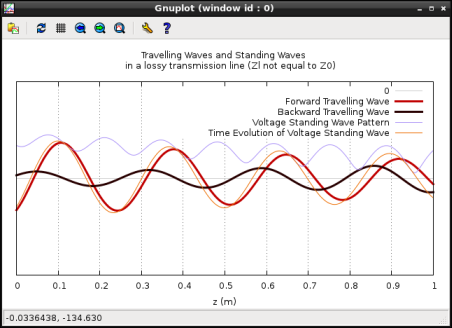
Formation of Standing Wave Patterns in a Lossless Open Circuited Transmission Line




Pure Voltage and Current Standing Wave Patterns in a Lossless Open Circuited Transmission Line


Theory behind Standing Waves and Standing Wave patterns

Signal energy is transmitted through a transmission line from the source or generator to the load or receiver in the form of voltage and current waves. At the load end, part of the signal is reflected back depending on the type of load impedance($Z_{L}$) and the characteristic impedance ($Z_{0}$) of the line. The ratio of $Z_{L}$ and $Z_{0}$ determines the reflection coefficient $\Gamma_{L}$ at the load end. The reflection coefficient, defined as the ratio of the reflected voltage to the incident voltage, however, assumes different values as one traverses down the line from the load end towards the source. If $V_{+}$ and $V_{-}$ be the amplitudes of the incident and reflected voltage waves in a transmission line of length $L$ and propagation constant $\gamma = \alpha + j\beta$ ($\alpha$ being the attenuation constant and $\beta$ being the phase constant of the line), then the reflection coefficient at any point $z$ from the sending end or equivalently at any point $d$ from the load end (where $d=L-z$) can be expressed through the following equations:


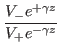$\displaystyle \Gamma (z)$ $\textstyle =$ $\displaystyle \frac{V_{-} e^{+\gamma z}}{V_{+} e^{-\gamma z}}$  
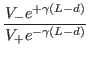$\displaystyle \Gamma (d)$ $\textstyle =$ $\displaystyle \frac{V_{-} e^{+\gamma (L-d)}}{V_{+} e^{-\gamma (L-d)}}$  
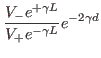  $\textstyle =$ $\displaystyle \frac{V_{-} e^{+\gamma L}}{V_{+} e^{-\gamma L}} e^{-2 \gamma d}$  
  $\textstyle =$ $\displaystyle \Gamma _{L} e^{-2 \gamma d}$  
  $\textstyle =$ $\displaystyle \vert\Gamma _{L}\vert e^{ j \theta_{L}} e^{-2 \gamma d}$  

Again, since the reflection coefficient at the load end can be expressed as:
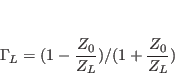\begin{displaymath} \Gamma_{L} & = & (1-\frac{Z_{0}}{Z_{L}})/(1+\frac{Z_{0}}{Z_{L}}) \nonumber \end{displaymath}  

we can obtain the value of the reflection coefficient $\Gamma (d)$, at any point from the load end, in terms of $\Gamma_{L}$. The standing wave is obtained by taking the superposition of the incident and reflected voltage waves as follows:
$\displaystyle V_{sw}$ $\textstyle =$ $\displaystyle V_{inc} + V_{ref}$  
  $\textstyle =$ $\displaystyle V_{+} e^{-\gamma z} + V_{-} e^{+\gamma z}$  
  $\textstyle =$ $\displaystyle V_{+} e^{-\gamma z}(1+ \Gamma (z))$  

The amplitude of the standing wave gives us the voltage standing wave pattern:
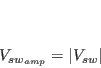\begin{displaymath} V_{sw_{amp}} & = & \vert V_{sw}\vert \nonumber \end{displaymath}  

If we follow the evolution of the standing wave with time, we will find that its amplitude ($\vert V_{sw}\vert$) oscillates between a maximum value ($V_{max}$) and a minimum value ($V_{min}$), every quarter wavelength apart, the wavelength being that of the voltage wave, $\lambda = v_{p}/\nu$. $\nu$ is the frequency of the signal being transmitted and $v_{p}$ is the phase velocity of the wave, the value of which is slightly less than the free space velocity ($c$) of an electromagnetic wave. The distance between two successive maxima or minima turns out to be $\lambda/2$. Since the position of points corresponding to $V_{max}$ and $V_{min}$ remain constant with time, the wave is called a standing wave.

Screen-shot of incident, reflected, standing waves and the standing wave pattern for a lossy line at a particular instant of time.
Screen-shot of incident, reflected, standing waves and the standing wave pattern
for a lossy line at a particular instant of time.

Figure 1. depicts how a standing wave pattern is generated from incident and reflected waves in a lossy ($\alpha \neq 0$) imperfectly terminated ($Z_L \neq Z0$) line. Since the line is lossy, $V_{max}$ and $V_{min}$ are not constant but a function of $z$, decreasing progressively with increasing $z$. If the line happened to be lossless ($\alpha=0$), then however $V_{max}$ and $V_{min}$ would have been constant throughout the length of the line.

If a line is terminated in an open circuit ($Z_{L}=\infty$), a short circuit ($Z_{L}=0$) or a pure reactive load like $Z_{L}$ equalling $-\frac{j}{\sqrt{3}} Z_{0}$, the whole of the incident energy at the load is reflected back ( $\vert\Gamma_{L}\vert=1$). The standing wave in all such cases is said to be a pure standing wave. Figure 2. depicts such a pure standing wave for a line terminated in an open circuit ($Z_L= \infty$, $\Gamma_{L}=+1$) and assumed lossless.

Screen-shot of incident, reflected, pure standing waves and the standing wave pattern for a lossless open circuited line at a particular instant of time.
Screen-shot of incident, reflected, pure standing waves and the standing wave pattern
for a lossless open circuited line at a particular instant of time.

For pure standing waves in lossless lines, $V_{max} = 2V_{+}$ and $V_{min} = 0$. The points corresponding to $V_{min}$, are now called the nodes and those corresponding to $V_{max}$ are called the antinodes. The instantaneous standing wave, though oscillating with time, is always zero ($V_{sw}(t)=0)$ at the nodes and its magnitude is always a maximum at the antinodes, equalling the amplitude ($V_{0}(t)$) of oscillation at the particular instant of time.

Thus we observe, that for standing waves (pure or impure) in any lossless line, $V_{max}$ and $V_{min}$ have the same value throughout the length of the line, and as such, are used to define a parameter called the Voltage Standing Wave Ratio (VSWR) or $\rho$ for the line as follows:

\begin{displaymath} \rho = \frac{V_{max}}{V_{min}} \nonumber \end{displaymath}  

In the case of a pure standing wave in a lossless line, $V_{max} = 2V_{+}$ and $V_{min} = 0$ so that $\rho=\infty$. It can be analytically shown that
\begin{displaymath} \rho = \frac{1+\vert\Gamma\vert}{1-\vert\Gamma\vert} \nonumber \end{displaymath}  

where $\Gamma$ has the same value throughout the (lossless) line and as such equals $\Gamma_{L}$.

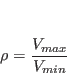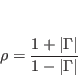So far we have been talking about voltage waves and voltage standing wave patterns. We could also obtain current standing waves if we superpose incident and reflected current waves travelling from the source toward the generator and vice versa respectively as follows:

$\displaystyle I_{sw}$ $\textstyle =$ $\displaystyle I_{inc} + I_{ref}$  
  $\textstyle =$ $\displaystyle I_{+} e^{-\gamma z} + I_{-} e^{+\gamma z}$  
  $\textstyle =$ $\displaystyle Y_{0} V_{+} e^{-\gamma z} - Y_{0} V_{-} e^{+\gamma z}$  
  $\textstyle =$ $\displaystyle Y_{0} V_{+} e^{-\gamma z}(1- \Gamma (z))$  

It is very important to note that the reflected current wave is opposite in phase to the reflected voltage wave. Pure voltage and current standing waves and the corresponding standing wave patterns for a lossless line, terminated with a pure reactance ( $-\frac{j}{\sqrt{3}} Z_{0}$) , are shown in Figure 3.
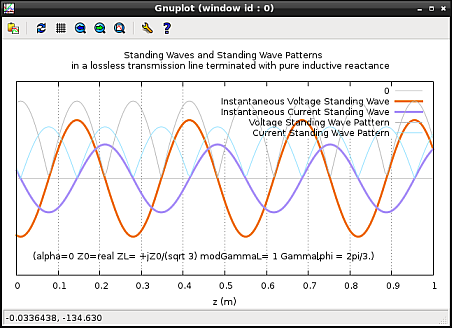
Screen-shot of pure voltage and current standing waves and the corresponding standing wave patterns for a lossless line terminated by a pure reactance at a particular instant of time.
Screen-shot of pure voltage and current standing waves and the corresponding
standing wave patterns for a lossless line terminated by a pure reactance
at a particular instant of time.
One may note that the voltage nodes and current antinodes coincide and successive voltage and current nodes (as also successive voltage and current antinodes) are spaced $\lambda/4$ apart.

Interestingly, if the transmission line is perfectly matched ($Z_L = Z0$), there is no reflected wave ($\Gamma = 0$). Such a line is called a flat line, since the standing wave patterns turn out to be a straight lines, as shown in Figure 4. VSWR or $\rho$ for such a line equals 1.

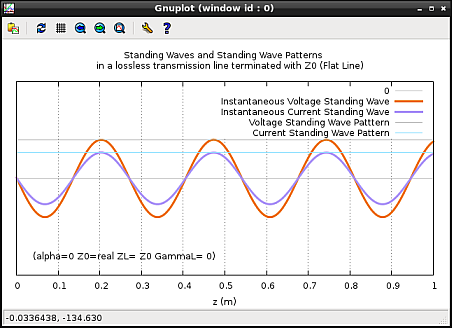
Screen-shot of voltage and current standing waves and the corresponding standing wave patterns for a lossless perfectly matched line at a particular instant of time.
Screen-shot of voltage and current standing waves and the corresponding
standing wave patterns for a lossless perfectly matched line at a
particular instant of time.



In conclusion, let us ask the question: What is the practical use of the VSWR?

VSWR is used in slotted line measurements of load impedances. A slotted section of a transmission line at the load end is considered for the purpose. A probe is used to sample the electric field and hence the voltage standing wave at different distances from the load and the position of the first voltage minimum ($d_{min}$) in the standing wave pattern is found. The reflection coefficient for a lossless line at a distance $d$ from the load end is given by:


$\displaystyle \Gamma (d)$ $\textstyle =$ $\displaystyle \Gamma _{L} e^{-2 \gamma d}$  
  $\textstyle =$ $\displaystyle \Gamma_{L} e^{-2 j \beta d}$  
  $\textstyle =$ $\displaystyle \vert\Gamma _{L}\vert e^{ j \theta_{L}} e^{-2 j \beta d}$ (1)
  $\textstyle =$ $\displaystyle \vert\Gamma_{L}\vert e^ {j\phi (d)}$  

where $\theta_{L}$ is the phase of the reflection coefficient at the load end and $\phi (d)$ is the phase of the reflection coefficient at the point $d$. Therefore,
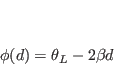\begin{displaymath} \phi (d) = \theta_{L} -2 \beta d \nonumber \end{displaymath}  

At the point of the first minimum ($d_{min}$), the incident and refelcted waves are in antiphase, implying $\phi (d) = -\pi$. Therefore $\theta_{L}$ can be found out to be $2 \beta d - \pi$ where $\beta = 2\pi/\lambda$.

On the other hand, $\vert\Gamma_{L}\vert$ can be obtained from VSWR measurements, implying we can then obtain $\Gamma_{L}$ which equals $\vert\Gamma _{L}\vert e^{ j \theta_{L}}$.

Finally, the load impedance can also be expressed in terms of $\Gamma_{L}$, as:

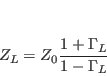\begin{displaymath} Z_{L} = Z_{0}\frac{1+\Gamma_{L}}{1-\Gamma_{L}} \nonumber \end{displaymath}  

Thus, with the knowledge of standing waves and the VSWR ($\rho$), one may obtain the load impedance ($Z_{L}$).


Go to page top

My main teaching page

© Abhijit Poddar All rights reserved.